
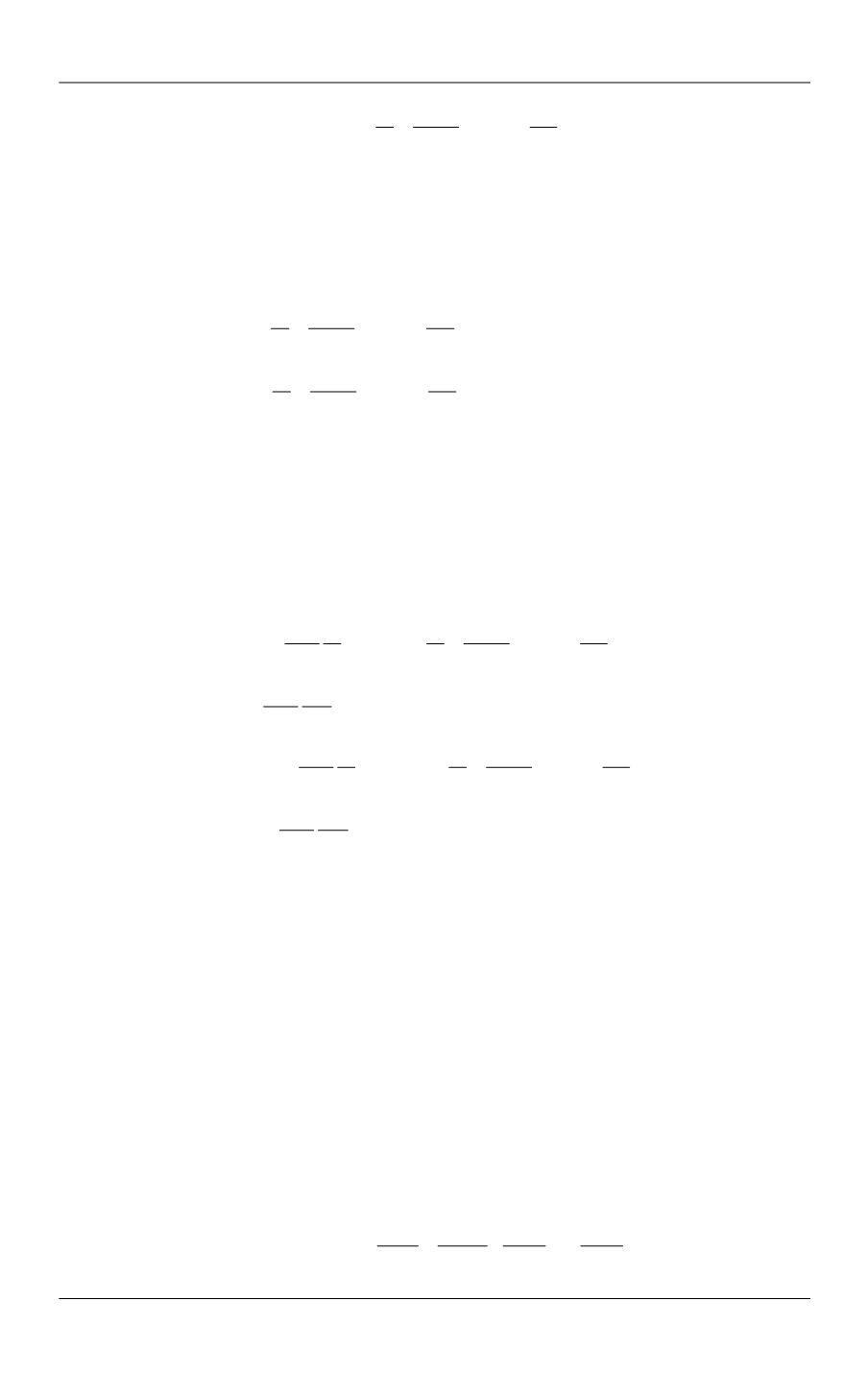
Уточненное решение системы дифференциальных уравнений в задаче изгиба…
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. Машиностроение. 2017. № 5
13
2
2
2
1
1
.
2 2
4
Z
Z
h M h
v
EJ
(13)
Аналогичные зависимости будут определять перемещения на линиях со-
единения остальных пластинок 2 и 3, 4 и 3, 4 и 1 между собой (см. рис. 1).
Объединим функции
,
i
i
i
прогибов (11) и (13) для каждой плас-
тинки:
2
2
1
2 2 2
1
2
2
3
4 4 4
3
;
,
0;
2 2
4
;
,
0.
2 2
4
Z
Z
Z
Z
h M h
EJ
h M h
EJ
(14)
С помощью найденных функций напряжений
,
i
i
i
(10) и прогибов
( , )
i
i
i
(14) для каждой отдельной пластинки можно построить решение для
системы дифференциальных уравнений (4) с граничными условиями (5).
Аналитическое решение для рассматриваемой системы дифференциальных
уравнений
(4) можно получить из разрешающих функций (10) и (14), которые
при изгибе прямого участка волновода примут вид:
2
2
2
1
1
1
1
3
2
2
2
2
2
2
3
3
3
3
3
4
4
4
;
;
4
2 2
4
;
0;
6
;
;
4
2 2
4
;
0.
6
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
M h
h M h
w
J
EJ
M
w
J
M h
h M h
w
J
EJ
M w
J
(15)
Используя выражения (15), можно определить напряжения и деформации в
любой точке
i
-й пластинки (
i
= 1, 2, 3, 4), составляющих прямой участок волно-
вода, при его изгибе.
Максимальные нормальные напряжения.
На обеспечение требований проч-
ности, жесткости и функционально-эксплуатационных характеристик волново-
дов существенное влияние будут оказывать максимальные напряжения, возни-
кающие как в отдельных пластинках, образующих прямоугольное поперечное
сечение, так и в местах их соединения.
Согласно теории пластин и оболочек, результирующие нормальные напря-
жения, действующие в любой
i
-й пластинке прямого участка волновода, будут
определяться суммой продольных
i
и изгибных
i
компонентов напряже-
ний [14]:
2
2
2
2
2
2
2
;
1
i
i
i
i
i
i
i
i
i
i
EZ
(16)
















