
А.В. Аттетков, И.К. Волков, Е.В. Пилявская
46
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. Машиностроение. 2017. № 3
ствами (15) и (18). Кроме того, при
2 2
1
k k
<
система (9) определяет единственную
точку покоя
(
)
0
0
, 0 .
O
= α
При
2 2
1
k k
=
появляется вторая точка покоя
( )
1
1, 0 ,
O
=
которая с ростом значения параметра
2
k
начинает «перемещаться» по отрезку,
соединяющему точки
(
)
0
1,
1
α −
и
(
)
0
, 0 ,
α
от точки
(
)
0
1,
1
α −
к точке
(
)
0
, 0 .
α
При
2
2
max
k k
=
точка покоя
( )
1
1, 0
O
=
«попадает» в точку покоя
(
)
0
0,
0 ;
O
= α
при
дальнейшем росте параметра
2
k
точка
( )
1
1, 0
O
=
«исчезает» из зоны анализа.
Значение параметра
2
max
,
k
определенного равенством (18), где функционал
( )
,
Φ γ δ
задан последним равенством (17), устанавливает условие существова-
ния минимальной скорости распространения УВ в двухфазном пористом мате-
риале:
(
)
(
)
(
)
[
]
1/2
0
min
1
0
2 1
.
3
1 1 1
Y
D
α −δ
=
ρ δ+α − + γ − δ
(19)
Ее появление физически обусловлено механическими свойствами фазы 1
изучаемого материала. При
0
δ =
равенство (19) известно [11, 12].
Точки покоя, определяемые системой (10).
Согласно (5), система (10) опре-
деляет единственную точку покоя
( )
1
1, 0 ,
O
=
которая всегда существует без-
относительно к значениям определяющих безразмерных параметров системы. Та-
ким образом, параметр
2
k
является бифуркационным параметром. При
(
) (
)
2
2
2
max
1
0,
,
k
k
k
∈ ∪ + ∞
система (10) имеет две точки покоя
( )
1
1, 0
O
=
и
(
)
0
0
, 0
O
= α
. При значении параметра
2
2
1
,
k k
=
где
2
1
k
определено равенством (15),
точка покоя
1
(1, 0)
O
становится двойной; с ростом значения параметра
2
k
из этой
точки «выходит» третья точка покоя
(
)
*
*
, 0
O
= α
и «начинает свое движение» по
оси
0
α
в направлении точки покоя
(
)
0
0
, 0 .
O
= α
При
2
2
max
,
k k
=
где
2
max
k
опреде-
лено равенством (18), точка
0
0
( , 0)
O
= α
становится уже двойной точкой покоя.
При дальнейшем росте параметра
2
k
вторая точка покоя «исчезает» из зоны
анализа.
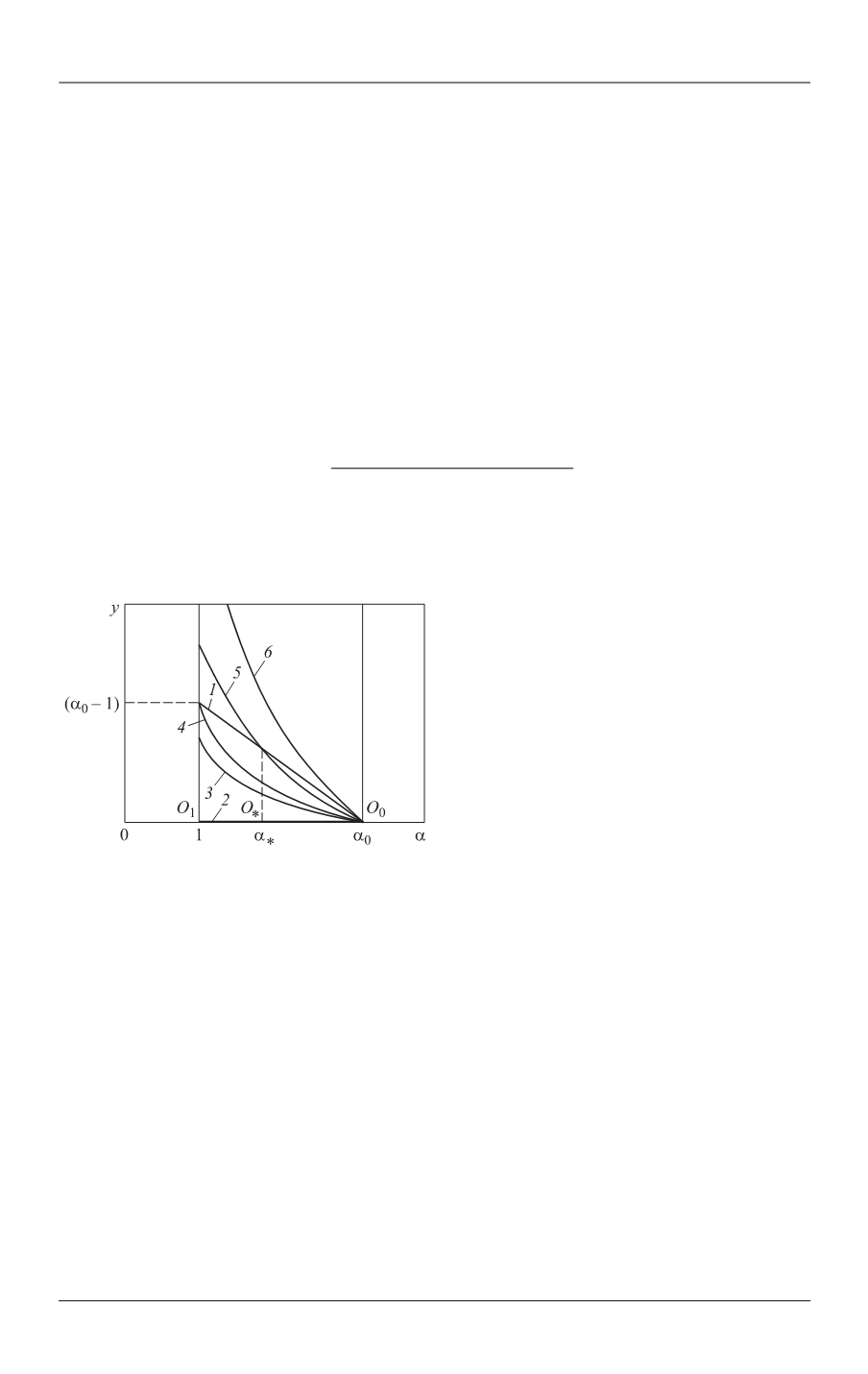
Зависимость положения третьей точки
покоя
*
O
изучаемой системы от значения
бифуркационного параметра
k
:
кривая
1
—
( )
1
;
y
= ϕ α
кривые
2–6 —
(
)
2
2
,
:
y
k
= ϕ α
2 —
2
0,
k
=
3 —
2
2
1
,
k k
<
4 —
2
2
1
,
k k
=
5 —
(
)
2
2 2
1 max
,
,
k k k
∈
6 —
2
2
max
k k
>
















