
Математическая модель прямолинейного движения по деформируемой опорной поверхности…
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. Машиностроение. 2017. № 2
129
упругих элементов (концы векторов всех нормальных реакций лежат в одной
плоскости) [10];
деформация грунта задается не через его непосредственные физические
характеристики, а как удельные потери энергии при качении колеса по ровному
основанию;
данные стационарных режимов переносятся на исследование неустано-
вившихся режимов качения движителей.
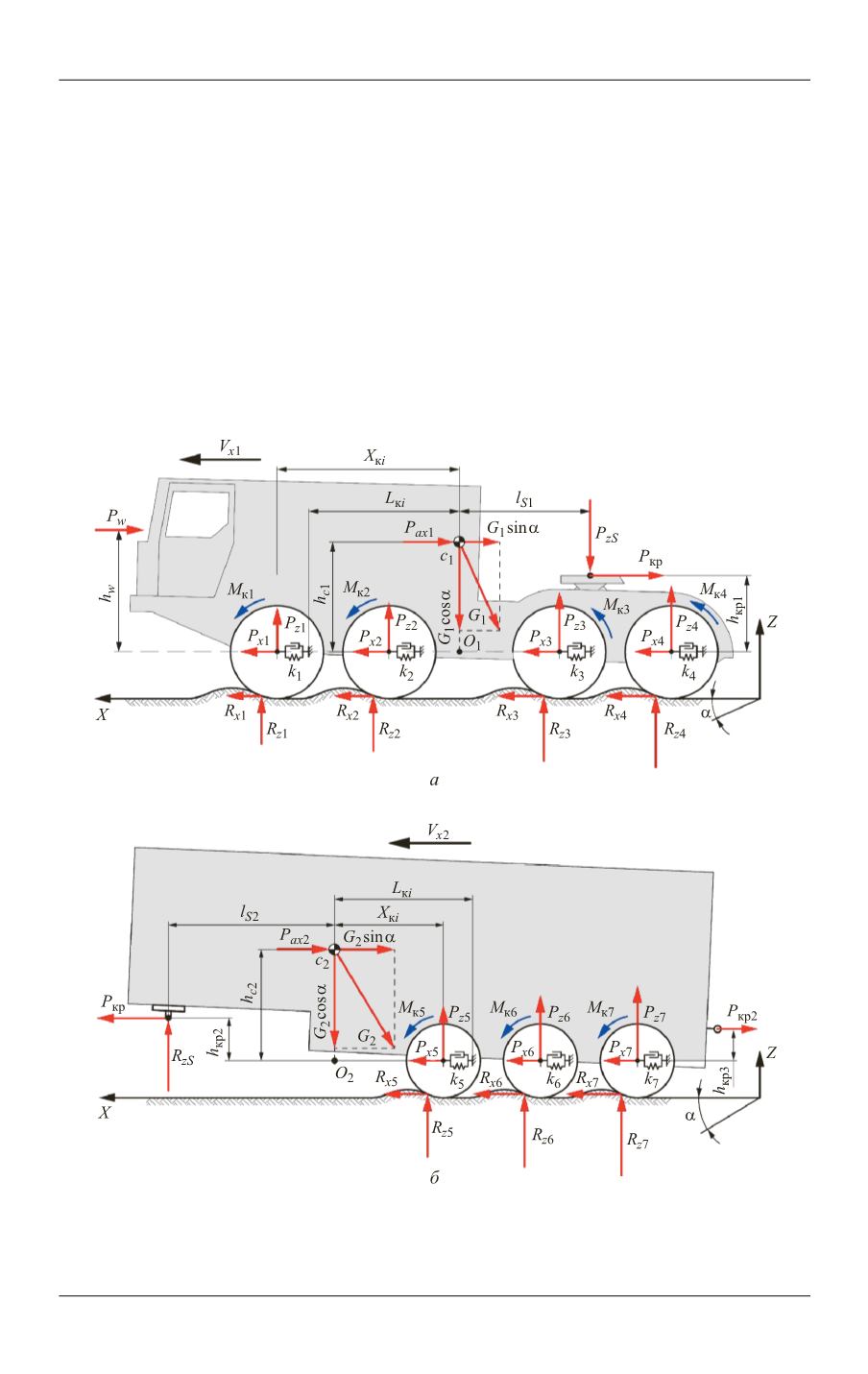
Построение математической модели движения седельного автопоезда рас-
смотрено на примере четырехосного автомобиля-тягача с индивидуальным
приводом колес и активного трехосного полуприцепа. Расчетная схема движе-
ния звеньев автопоезда, представленная на рис. 7, принята с учетом характера
решаемой задачи и описывается соответствующими уравнениями динамики (5):
Рис. 7.
Расчетная схема движения звеньев автопоезда по деформируемому опорному
основанию:
а
— полноприводный тягач;
б
— активный (полноприводный) полуприцеп
















