
В.А. Горелов, Б.В. Падалкин, О.И. Чудаков
128
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. Машиностроение. 2017. № 2
к
к к
к
б
к.c
;
1
,
x
z
x
w
z
mV P P
J
M S f
P r
(4)
где
m
— масса, приходящаяся на колесо;
к
x
V
— продольное ускорение центра
масс колеса;
J
k
— момент инерции колеса относительно оси вращения;
к
— уг-
ловое ускорение колеса.
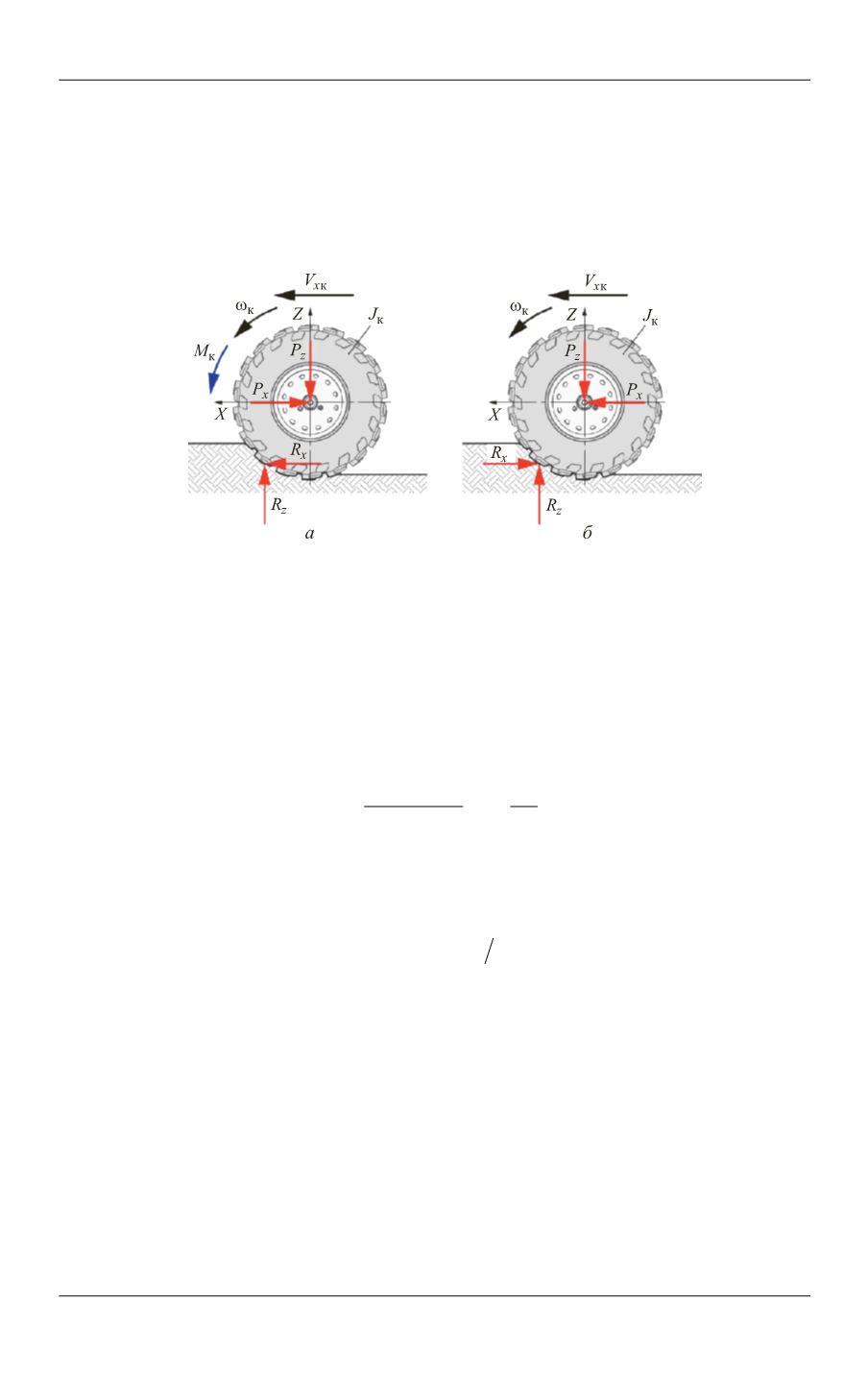
Рис. 6.
Расчетная схема движения колеса по деформируемому опорному основанию:
а, б
— ведущий и ведомый режимы
В настоящей работе приведенный в [6] подход к моделированию взаимо-
действия движителя на ведущем режиме с деформируемой опорной поверхно-
стью распространяется также на случай ведомого режима. Сделано допущение о
том, что при определении коэффициента буксования (юза) при качении ведо-
мого колеса в случае бульдозерного вытеснения грунта можно воспользоваться
зависимостью для тормозного режима качения:
к к к.с
к.с
б
к
к
1 .
x
x
V r
r
S
V
r
Соответственно система уравнений для качения колеса на ведомом режиме
будет иметь вид
к
к к
к.c
б
;
1 .
x
x
z
w z
mV P P
J
f P r
S
Математическая модель движения автопоезда.
Для решения широкого
круга задач, связанных с тяговой динамикой и проходимостью, создана матема-
тическая модель движения двухзвенного седельного автопоезда. При разработ-
ке математической модели сделаны следующие основные допущения:
рассматривается прямолинейное движение автопоезда по ровному де-
формируемому опорному основанию;
система симметрична относительно продольной оси автопоезда, т. е.
условия движения левого и правого бортов одинаковые;
колеса одного борта также находятся в одинаковых условиях;
определение нормальных реакций движителей при взаимодействии с
опорной поверхностью происходит с допущением о совместности деформаций
















