
координат
Ox
1
x
2
x
3
, а затем пересчитываются в системе координат
O
ˉ
x
1
ˉ
x
2
ˉ
x
3
:
V
∗
0
= Λ
∗
V
0
;
ω
∗
= Λ
∗
ω
;
˙V
∗
0
=
d
Λ
∗
dt
V
0
+ Λ
∗
˙V
0
;
˙
ω
∗
=
d
Λ
∗
dt
ω
+ Λ
∗
˙
ω
;
d
Λ
∗
dt
=
d
Λ
∗
ds
|
V
0
(
t
)
|
.
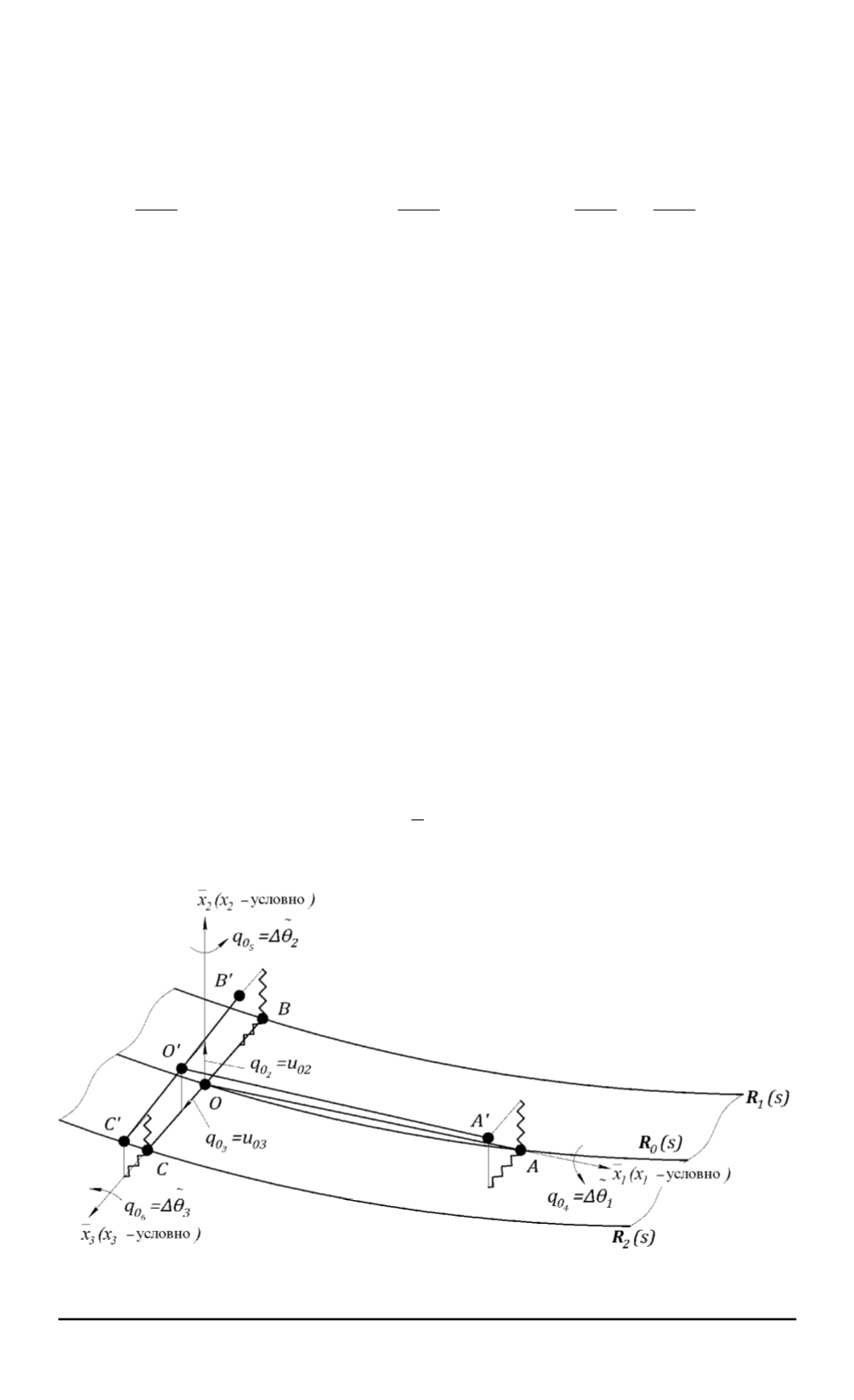
Учет упругости и демпфирования роликов.
За счет упругости
и демпфирования роликов тележка будет совершать дополнительные
движения как твердое тело с пятью степенями свободы относительно
подвижной системы координат
Ox
1
x
2
x
3
или
O
ˉ
x
1
ˉ
x
2
ˉ
x
3
. В качестве обоб-
щенных координат, представляющих эти движения, будем рассматри-
вать: перемещения
q
0
2
=
u
02
,
q
0
3
=
u
03
полюса (точки
O
) вдоль коор-
динатных осей
x
2
,
x
3
(или
ˉ
x
2
,
ˉ
x
3
) и углы поворота тележки
q
0
4
= Δ ˜
θ
1
,
q
0
5
= Δ ˜
θ
2
,
q
0
6
= Δ ˜
θ
3
в квадратичном приближении (
sinΔ ˜
θ
i
≈
Δ ˜
θ
i
,
cos Δ ˜
θ
i
≈
1
−
Δ ˜
θ
2
i
/
2
,
i
= 1
,
2
,
3
) относительно осей
x
1
,
x
2
,
x
3
(или
относительно осей
ˉ
x
1
,
ˉ
x
2
,
ˉ
x
3
) (рис. 2).
В результате точки
O
,
A
,
B
и
C
, которые по-прежнему связаны с
траекторией движения, смещаются в точки
O
0
,
A
0
,
B
0
и
C
0
, которые
в данном случае характеризуют положение тележки после введения
упругостей роликов, т.е.
O
0
A
0
=
l
и
B
0
C
0
= 2
a
(смещения точек
B
и
C
по оси
x
3
или
ˉ
x
3
равны).
В этом случае вектор дополнительных перемещений твердого тела,
обусловленных упругими деформациями роликов, будет иметь вид
˜u =
6
X
i
=2
q
0
i
ϕ
0
i
+
1
2
6
X
i
=4
6
X
j
=4
q
0
i
q
0
j
ψ
0
i
0
j
,
Рис. 2. Схема учета упругости и демпфирования роликов
104 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2016. № 2
















