
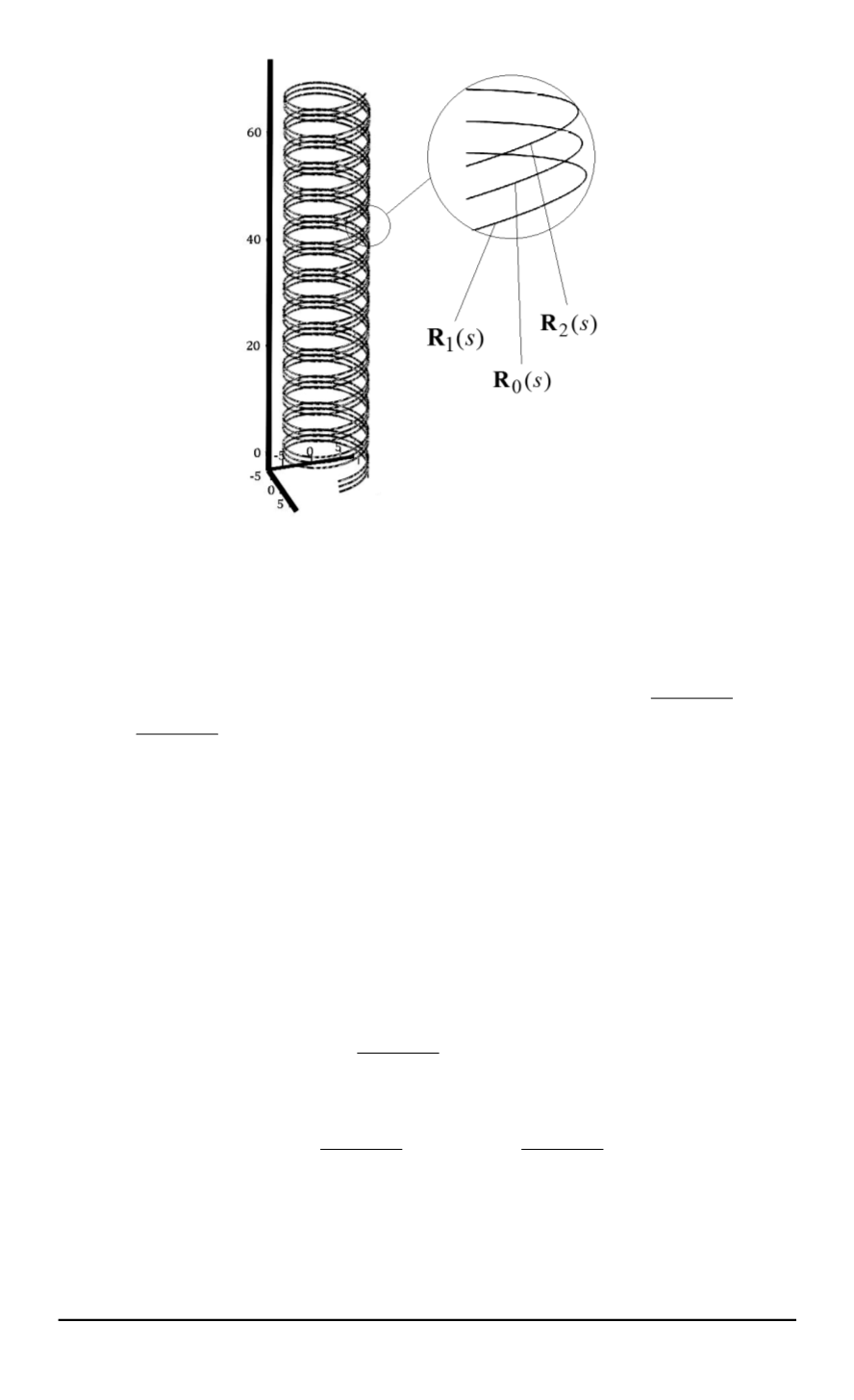
Рис. 3. Общий вид траектории движения
R
— радиус винтовой линии (радиус цилиндрической образую-
щей);
λ
— шаг подъема винтовой линии за угол поворота
ϕ
, рав-
ный 1 рад (
2
πλ
— подъем за один виток) (рис. 3). В любой точке
винтовой линии касательная
t
, нормаль
n
и бинормаль
b
име-
ют следующие координаты (здесь и далее
ˉ
R
=
R
√
R
2
+
λ
2
,
ˉ
λ
=
=
λ
√
R
2
+
λ
2
):
t
=
−
ˉ
R
sin
ϕ
ˉ
R
cos
ϕ
ˉ
λ
T
;
n
=
−
cos
ϕ
−
sin
ϕ
0
T
;
b
= ˉ
λ
sin
ϕ
−
ˉ
λ
cos
ϕ
ˉ
R
T
.
Матрица
Λ
, как матрица направляющих косинусов единичных век-
торов
t
,
n
и
b
(без использования углов
θ
1
,
θ
2
и
θ
3
), записывается в
следующем виде:
Λ =
−
ˉ
R
sin
ϕ
ˉ
R
cos
ϕ
ˉ
λ
−
cos
ϕ
−
sin
ϕ
0
ˉ
λ
sin
ϕ
−
ˉ
λ
cos
ϕ
ˉ
R
.
Функциональная связь между длиной дуги
s
(она отсчитывается от
точки
M
(
R,
0
,
0)
при
ϕ
= 0
) и углом закрутки
ϕ
выражается следу-
ющим образом:
s
(
ϕ
) =
ϕ
√
R
2
+
λ
2
. Кривизна
κ
(
s
)
и кручение
æ(
s
)
винтовой линии в любой ее точке постоянны и равны [10]
κ
(
s
) =
R
R
2
+
λ
2
; æ(
s
) =
λ
R
2
+
λ
2
.
Поскольку подвижная система координат
Ox
1
x
2
x
3
связана с трех-
гранником Френе, то вектор мгновенной угловой скорости
ω
может
быть определен через векторное соотношение
ω
= æ
t
+
κb
. Посколь-
ку матрица
Λ
и вектор
ω
в данном примере могут быть записаны
106 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2016. № 2
















