
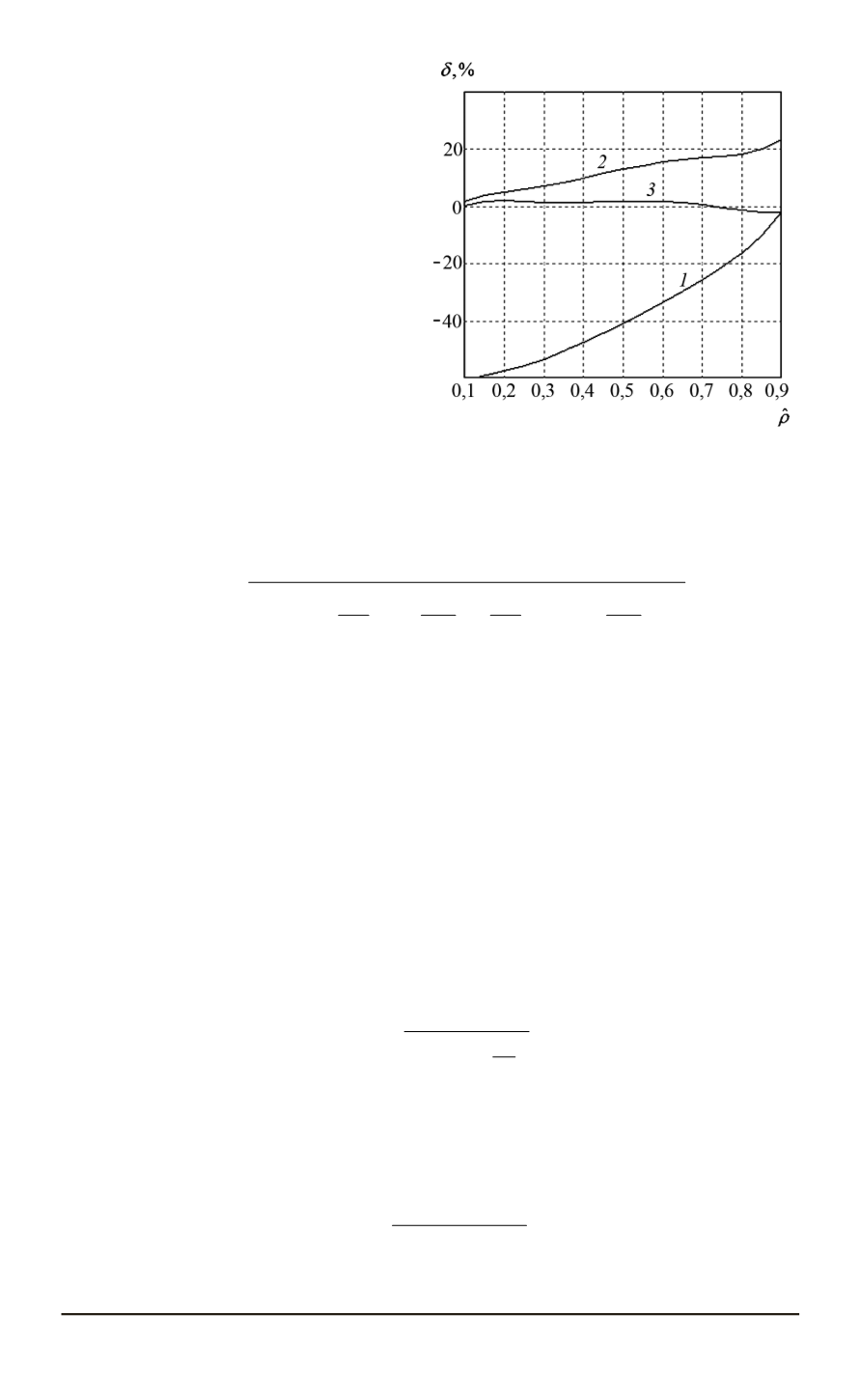
Рис. 7. Изменение относительной
погрешности определения
ˆ
ρ
m
от-
носительно шестигрупповой моде-
ли для классической модели мгно-
венного скачка (кривая
1
), для
шестигрупповой модели с обрат-
ной связью (кривая
2
), для расче-
та по формуле (9) (кривая
3
)
Нахождение максимального значения плотности нейтронов из
условия
dn/dt
= 0
для выражения (3) с учетом второго уравнения си-
стемы (1) и выражения для
λ
(
ρ
)
в форме (2) приводит к соотношению
n
max
=
λ
m
ˆ
ρ
m
β
αk
1 +
a
1
λ
m
+
2
a
2
λ
m
−
a
1
λ
m
ˆ
ρ
m
−
2
a
2
λ
m
ˆ
ρ
2
m
.
(7)
Анализ численных значений коэффициентов полинома в знамена-
теле показывает, что свободный член
1 +
a
1
/λ
m
заметно превышает
значения членов с первой и второй степенями
ˆ
ρ
m
. Это справедливо
в достаточно широкой области изменения начального возмущения по
реактивности за исключением лишь области, непосредственно приле-
гающей к мгновенной критичности, тем более, что имея различные
знаки, эти члены взаимно снижают влияние на окончательный резуль-
тат.
Это дает основание при невозможности получения корректного
решения пренебречь в первом приближении их вкладом. Тогда соот-
ношение (7) превращается в достаточно простое выражение
n
max
=
λ
ˆ
ρ
m
β
αk
h
1 +
a
1
λ
i
.
Рассматривая это выражение совместно с зависимостью (5) для
плотности нейтронов при
ρ
=
ρ
m
, которое при использовании норми-
рованных величин реактивности
ˆ
ρ
=
ρ/β
имеет вид
n
max
=
λ
(ˆ
ρ
2
0
−
ˆ
ρ
2
m
)
2
αk
(1
−
ˆ
ρ
m
)
β,
(8)
получаем квадратное уравнение относительно
ˆ
ρ
m
, решением которого
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение” 2015. № 3 37

















