
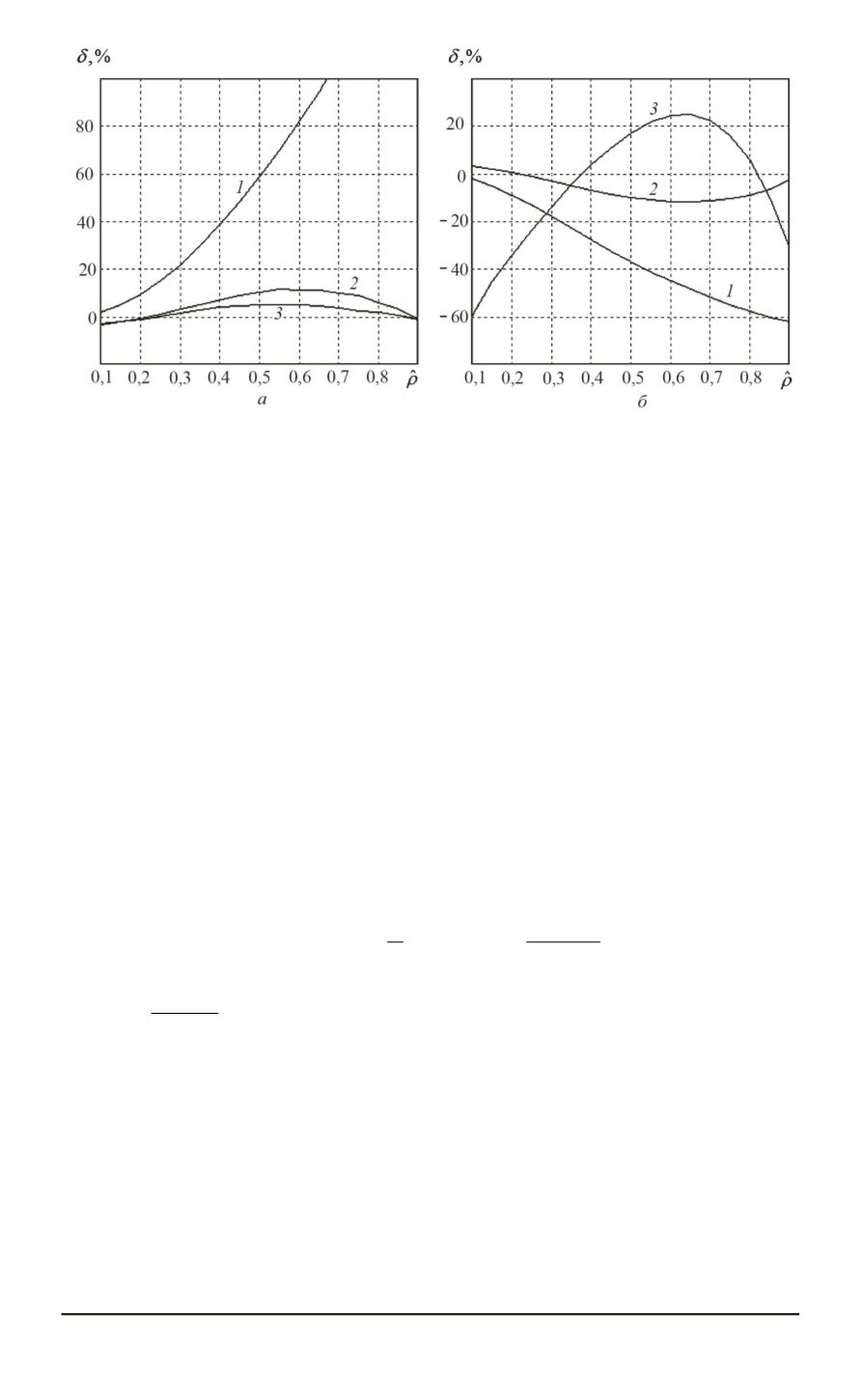
Рис. 9. Изменение относительной погрешности оценки длительности импульса
согласно [1] (
а
) и времени наступления максимума плотности нейтронов (
б
)
относительно шестигрупповой модели для классической модели мгновенного
скачка (кривые
1
), модифицированной одногрупповой модели (кривые
2
) и
расчета по формулам (8), (10) и (11) (кривые
3
)
формулам (8) и (10) дают еще меньшую погрешность (кривая
3
). В то
же время погрешности определения этого параметра для классиче-
ской модели мгновенного скачка достигают недопустимых значений
(кривая
1
).
Аналогичные проблемы, обусловленные отсутствием аналитиче-
ского решения, возникают и при оценке времени достижения макси-
мального значения плотности нейтронов
t
m
. В исследованном интер-
вале возмущений
0
,
1
<
ˆ
ρ <
0
,
9
он изменялся от 500 с до 20 с. В работе
[7] предложено полуэмпирическое соотношение для определения ана-
логичного параметра для модели Нордгейма – Фукса, которое показало
малый уровень погрешности сравнительно с теоретическим решением
модели Нордгейма – Фукса
t
m
=
t
1
+
t
2
=
1
ω
1
,
75 + ln
`ω
2
2
αKn
0
,
(11)
где
ω
=
λρ
0
β
−
ρ
0
— обратный начальный период.
Коэффициент 1,75, используемый в формуле, обусловлен исполь-
зованием теоретического решения при определении длительности им-
пульса. Определение длительности импульса через соотношение меж-
ду энергией импульса и длительностью требует значения 2 для этого
коэффициента [1].
Рассчитанная по формуле (11) с коэффициентом 2 зависимость вре-
мени наступления максимума плотности нейтронов при сравнении с
результатами расчетов по шестигрупповой модели дает зависимость
погрешности от возмущения, представленную на рис. 9,
б
(кривая
3
).
40 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2015. № 3

















