
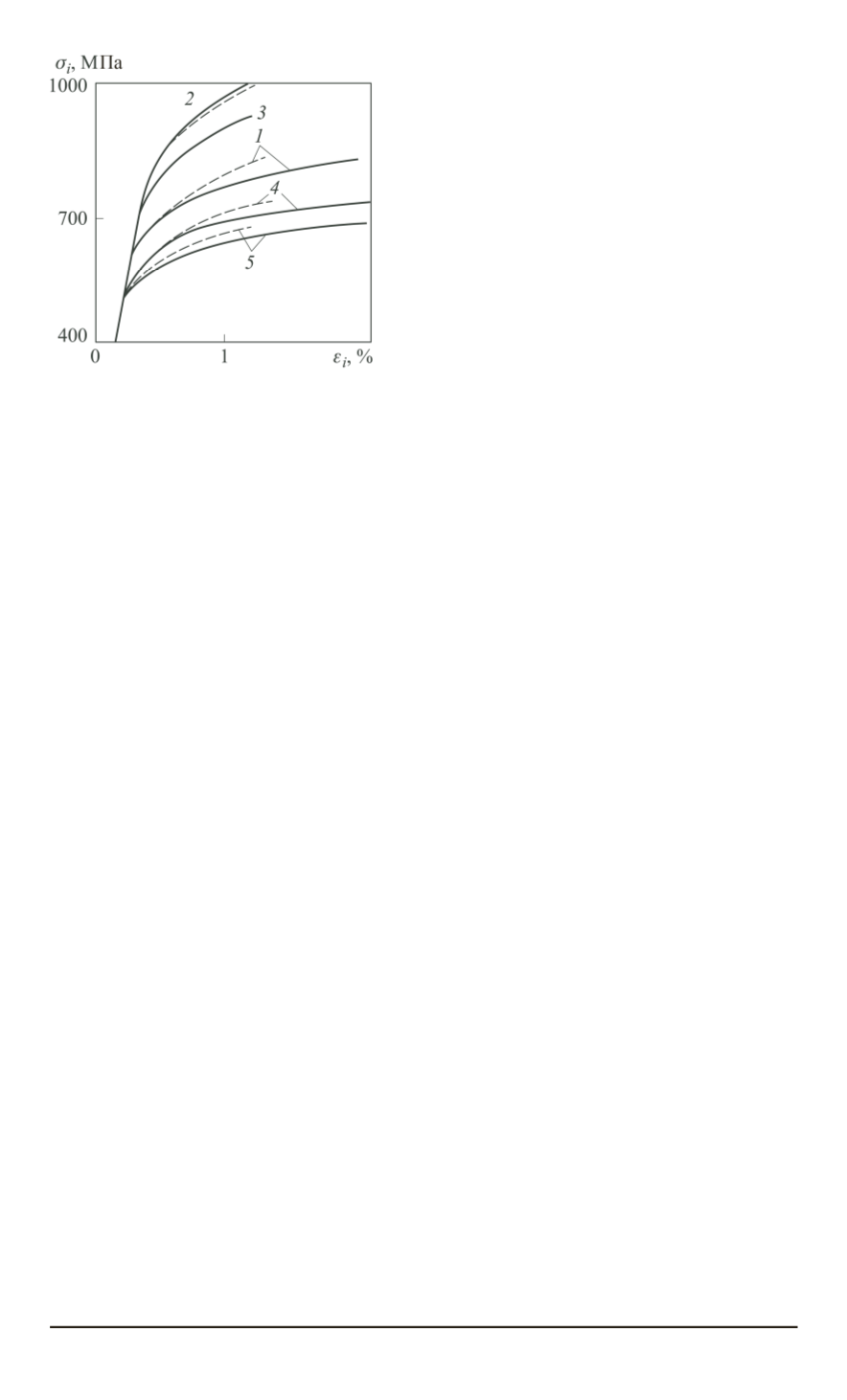
Диаграмма деформирования сред-
неуглеродистой стали
кривая
3
— чистому сдвигу, кривые
4
,
5
— двухосному растяжению при
σ/σ
i
= 0
,
577
; 0,667. Здесь
σ
i
— ин-
тенсивность напряжений. Диаграммы
представлены в координатах — обыч-
ные интенсивности напряжений
σ
i
и
деформаций
ε
i
. За опорную кривую,
по которой проводились описанные
ранее расчеты, бралась кривая для чи-
стого сдвига.
Проведенные расчеты для анало-
гичных экспериментальных данных
показали, что предложенная модель
может быть использована для описа-
ния нелинейного поведения некоторых разносопротивляющихся мате-
риалов. Очевидно, что возможность использования данного подхода
должна анализироваться в каждом конкретном случае.
Автор благодарит профессора МГТУ им. Н.Э. Баумана В.С. Зару-
бина за полезные замечания.
ЛИТЕРАТУРА
1.
Мясников В.П.
,
Олейников А.И.
Основы механики гетерогенно-
сопротивляющихся сред. Владивосток: Дальнаука, 2007. 172 с.
2.
Мэтьюз Ф.
,
Ролингс Р.
Композитные материалы. М.: Техносфера, 2004. 408 с.
3.
Максимов Р.Д.
,
Плуме Э.З.
,
Янсонс Ю.О.
Сравнительное исследование механи-
ческих свойств термореактивного полимера при растяжении и сжатии // Меха-
ника композитных материалов. 2005. Т. 41. № 5. С. 633–650.
4.
Бессонов Д.Е.
,
Зезин Ю.П.
,
Ломакин Е.В.
Разносопротивляемость зернистых
композитов на основе ненасыщенных полиэфиров // Изв. Саратовского ун-та.
Сер. Математика. Механика. Информатика. 2009. Т. 9. Вып. 4. Ч. 2. С. 9–13.
5.
Бессонов Д.Е.
,
Ершова А.Ю.
,
Зезин Ю.П.
,
Мартиросов М.И.
,
Рыбинский Л.Н.
Экспериментальное исследование деформирования и разрушения зернистых
композитов на основе полиэфирных смол // Механика композиционных ма-
териалов и конструкций. 2008. Т. 14. № 1. С. 111–125.
6.
Пахомов Б.М.
Условие пластического течения, включающее коэффициент Пуас-
сона // Вестник МГТУ им. Н.Э. Баумана. Сер. Машиностроение. 2014. № 2.
С. 15–27.
7.
Пахомов Б.М.
Применение теории собственных напряжений к описанию нели-
нейного деформирования металлов и сплавов // Инженерный журнал: наука и
инновации. 2013. Вып. 7. URL:
http://engjournal.ru/catalog/machin/rocket/854.html8.
Хажинский Г.М.
Деформирование. Разрушение. Надeжность. Задачи дефор-
мирования и разрушения стали. Методы оценки прочности энергетического
оборудования и трубопроводов / М.: Эдиториал УРСС, 2014. 544 с.
9.
Зарубин В.С.
,
Кувыркин Г.Н.
Математические модели механики и электродина-
мики сплошной среды. М.: Изд-во МГТУ им. Н.Э. Баумана, 2008. 512 с.
10.
Остросаблин Н.И.
Анизотропия и общие решения уравнений линейной теории
упругости. Дисс. . . . д-ра техн. наук. Тула, 2000. 215 с.
104 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2015. № 2

















