
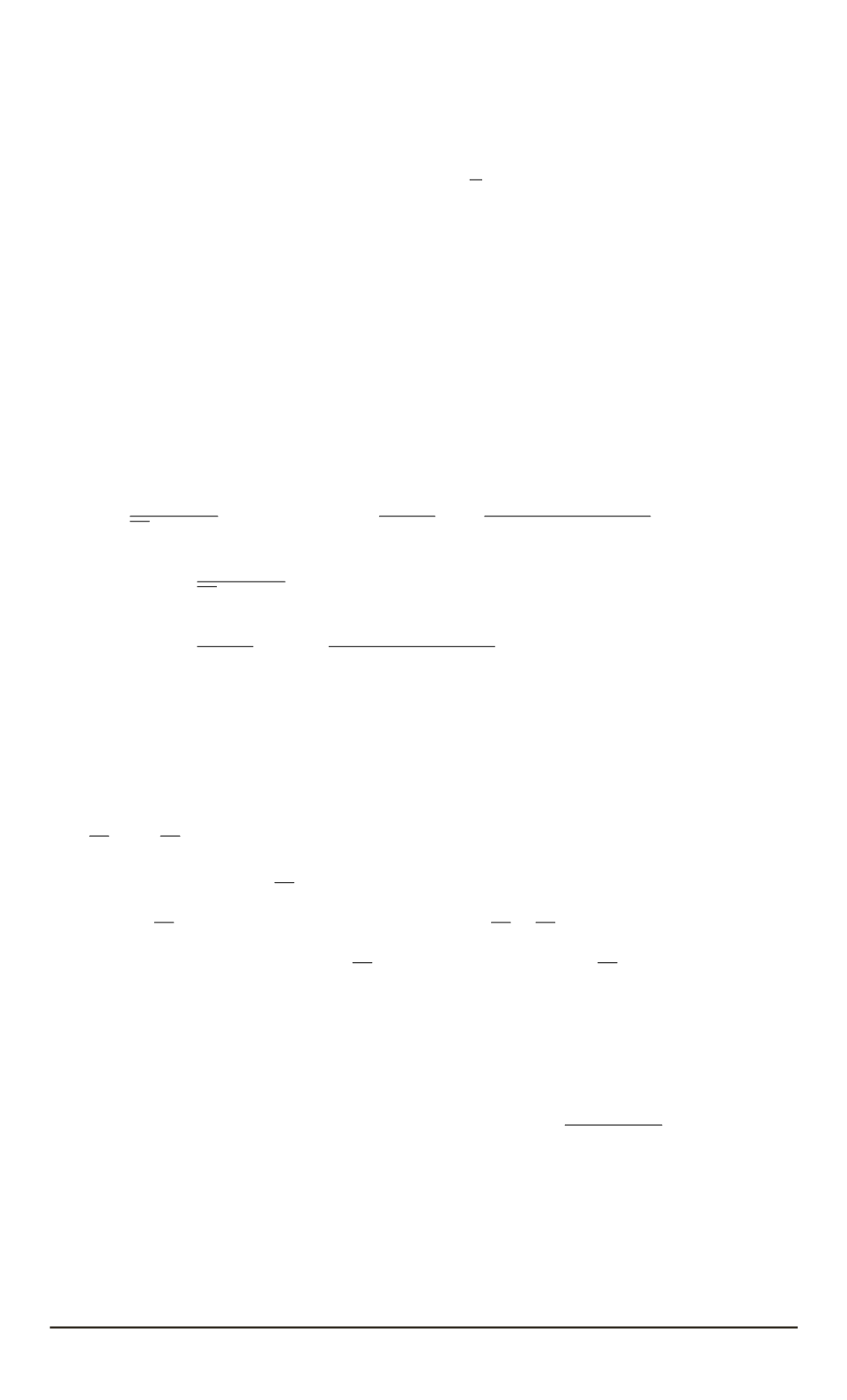
Если считать, что модуль упругости
E
всегда должен быть боль-
ше нуля, то, используя выражения (2), получаем границы изменения
коэффициента Пуассона для изотропного линейно-упругого материала
−
1
≤
ν
≤
1
2
.
У некоторых разносопротивляющихся материалов (например, у се-
рых чугунов) наблюдается разрыхление, т.е. пластическое увеличение
объема при сжимающих нагрузках. Если не отказываться от условия
положительности
U
, оставаясь в рамках описанной ранее модели де-
формационного типа, то описать “разбухание” материала при сжатии
невозможно. Развитие данного подхода применительно к таким мате-
риалам возможно, но не является темой настоящей работы.
При разгрузке напряжения
σ
ij
,
Q
и
p
ij
будут равны:
Q
=
L
G
0
+ 3
L
σ
+
L
Δ
ε
(
p
)
=
ν
1 +
ν
σ
+
Eν
(1 +
ν
) (1
−
2
ν
)
Δ
ε
(
p
)
;
p
ij
=
σ
ij
−
L
G
0
+ 3
L
σδ
ij
−
L
Δ
ε
(
p
)
δ
ij
;
p
ij
=
σ
ij
−
ν
1 +
ν
σδ
ij
−
Eν
(1 +
ν
) (1
−
2
ν
)
Δ
ε
(
p
)
δ
ij
.
(15)
Подставив выражения для собственных напряжений в условие начала
текучести
p
i
=
τ
∗
u
, где
τ
∗
u
— значение предела текучести на сдвиг,
достигнутое к началу разгрузки, получим условие текучести для по-
вторного нагружения
G
2
0
+ 4
G
0
L
+ 6
L
2
σ
2
xx
+
σ
2
yy
+
σ
2
zz
−
−
2
L
2
G
0
+ 3
L
(
σ
xx
σ
yy
+
σ
yy
σ
zz
+
σ
zz
σ
xx
) +
+ 2(
G
0
+ 3
L
)
2
σ
2
xy
+
σ
2
yz
+
σ
2
zx
−
2
G
0
G
0
+ 3
L Lσ
Δ
ε
(
p
)
+
+ 3
L
2
(
G
0
+ 3
L
)
2
(Δ
ε
(
p
)
)
2
= 2(
G
0
+ 3
L
)
2
τ
2
∗
u
(16)
или через модуль упругости
E
и коэффициент Пуассона
ν
1 + 2
ν
2
σ
2
xx
+
σ
2
yy
+
σ
2
zz
−
2
ν
(2
−
ν
) (
σ
xx
σ
yy
+
σ
yy
σ
zz
+
σ
zz
σ
xx
) +
+ 2(1 +
ν
)
2
σ
2
xy
+
σ
2
yz
+
σ
2
zx
−
2
Eνσ
Δ
ε
(
p
)
+
3
E
2
ν
2
(1
−
2
ν
)
2
(Δ
ε
(
p
)
)
2
=
= 2(1 +
ν
)
2
τ
2
∗
u
.
(17)
В пространстве главных напряжений
σ
1
,
σ
2
,
σ
3
уравнения (16) и
(17) определяют эллипсоид вращения, у которого наибольший из глав-
ных диаметров равнонаклонен к координатным осям, а координаты
96 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2015. № 2

















