
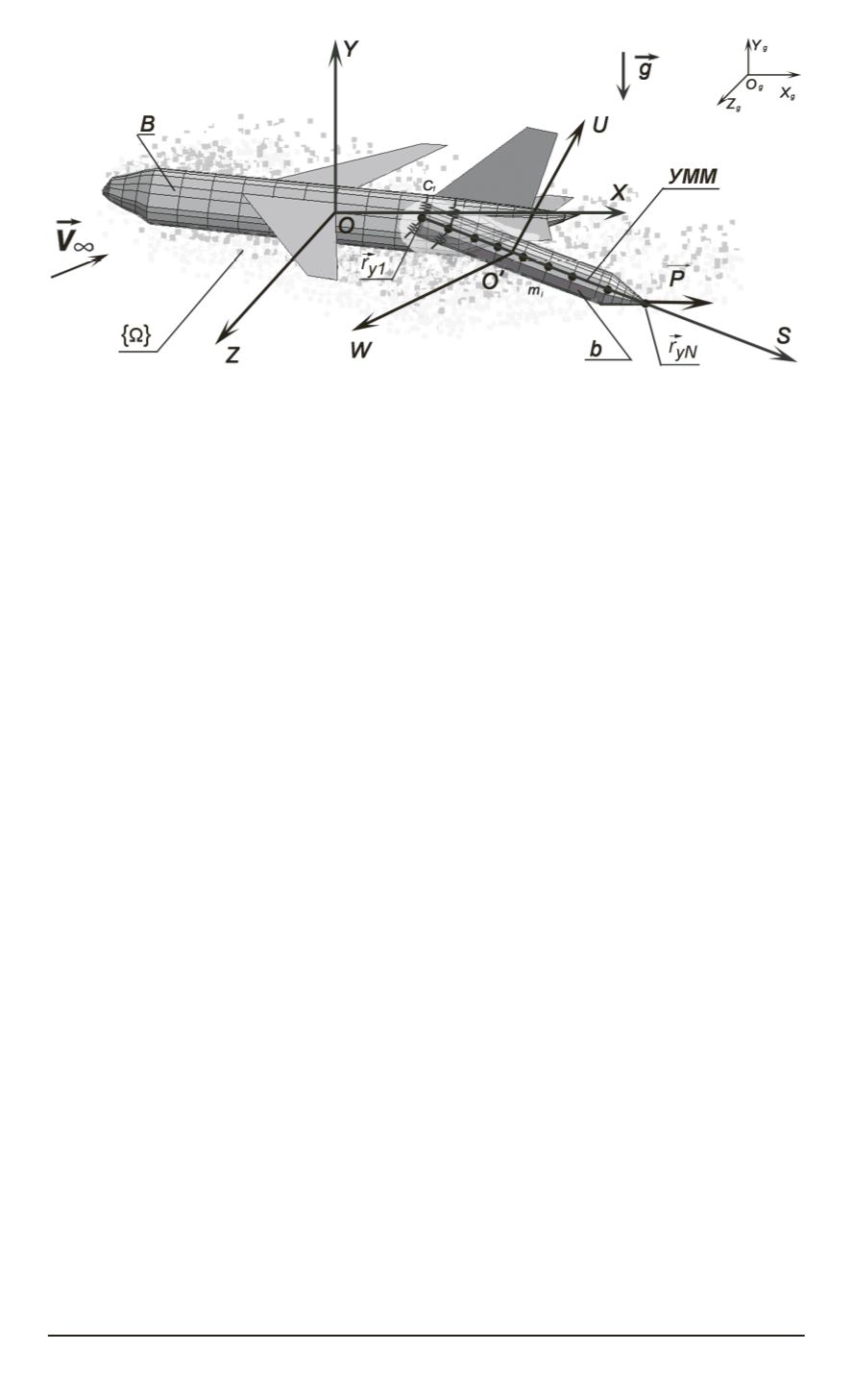
Рис. 1. Расчетная схема задачи
Примем, что среда имеет настолько малую вязкость, что при моде-
лировании можно использовать подход Прандля: эффекты вязкости
учитываются только вблизи обтекаемой поверхности как причина ге-
нерации завихренности, а в области течения среда рассматривается как
идеальная. Вектор ускорения свободного падения
~g
направлен вдоль
O
g
Y
g
. За счет выполнения маневра “Горка” РН разгружена вертикаль-
ной перегрузкой
n
y
, что учитывается как
|
~g
|
=
n
y
g
.
Самолет-носитель моделируется абсолютно жестким телом
B
, с
которым связана нормальная прямоугольная инерциальная система
координат
OXY Z
. Ракета-носитель моделируется телом вращения
b
. Введем подвижную систему координат
O
0
SUW
(орты
~i
b
, ~j
b
, ~k
b
),
связанную с центром масс
b
. Продольная ось ракеты
O
0
S
в началь-
ный момент времени совпадает с
OX
. Положение
O
0
SUW
относи-
тельно
OXY Z
определяется радиусом-вектором
OO
0
центра масс
~R
0
=
{
X
C
, Y
C
, Z
C
}
т
, а ориентация — углами Эйлера
{
γ, ϑ, ψ
}
т
.
Ракета считается упругодеформируемой по балочной модели.
С осью
b
связана упруго-массовая модель (УММ), состоящая из
N
сосредоточенных масс
m
i
, соединенных невесомыми балочными
элементами. Положение сосредоточенных масс в
O
0
SUW
задается
радиусами-векторами
~r
yi
=
s
i
~i
b
+
u
i
~j
b
+
w
i
~k
b
, где
s
i
— координата узла
в положении равновесия,
u
i
, w
i
— перемещения узлов при деформации.
Пусковая установка упрощенно моделируется линейными упруго-
вязкими связями с жесткостью
c
i
=
H
(
X
л
−
X
i
)
C
i
, где
H
(
x
)
— функция
Хевисайда и декрементом колебаний
n
i
. Координата рампы люка СН,
где происходит обрыв связей, обозначена как
X
л
. После обрыва всех
связей (
X
1
≥
X
л
) тело
b
движется под действием силы тяжести и
нестационарных аэродинамических сил до момента окончания расчета
t
=
t
k
.
Ракета-носитель из СН десантируется под действием внешней си-
лы
~P
, направленной вдоль
OX
, которая прикладывается к узлу
i
= 1
24 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2015. № 1

















