
координате
Z
C
приведен на рис. 4,
в
. Здесь график
γ
0
3
(
t
k
)
(сплошная
линия), отражающий наиболее вероятное движение ракеты, незначи-
тельно отклоняется от нуля. Однако случайный разброс бокового дви-
жения центра масс ракеты составляет в конце переходного режима
более полуметра. Графики границ области разброса параметра симме-
тричны относительно оси абсцисс, что показывает возможность ухода
ракеты как влево, так и вправо по ходу десантирования.
Графики углового отклонения РН в процессе десантирования пред-
ставлены на рис. 5, где также сплошной линией показано наиболее
вероятное движение
γ
0
i
(
t
k
)
, а штриховыми — границы областей раз-
броса.
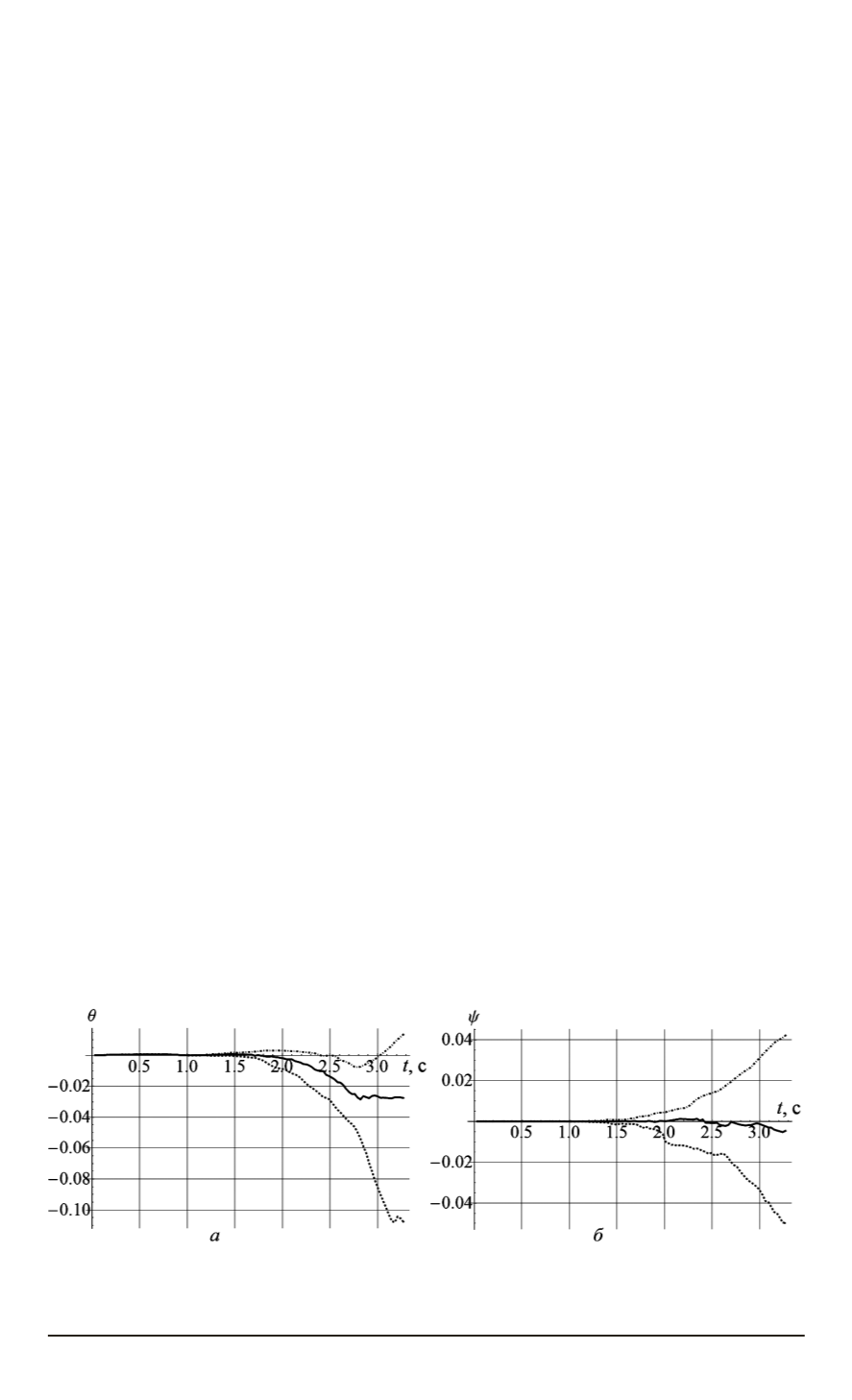
График отклонения ракеты по углу тангажа
ϑ
приведен на рис. 5,
а
.
Наиболее вероятный угол отклонения ракеты составляет в конце пе-
реходного режима порядка
γ
0
4
(
t
k
)
≈ −
1
,
7
◦
. Случайный разброс соста-
вляет от – 5,7
◦
до + 0,5
◦
. График отклонения ракеты по углу рыскания
ψ
приведен на рис. 5,
б
. Наиболее вероятный угол отклонения раке-
ты
γ
0
5
(
t
k
)
является практически нулевым. Однако случайный разброс
составляет
±
2
,
9
◦
.
Обсуждение полученных результатов.
Полученные в ходе чи-
сленного моделирования результаты позволили проанализировать ки-
нематику движения РН вблизи СН с учетом случайного разброса па-
раметров. Несмотря на то, что полученный разброс кинематических
параметров относительно невелик (разброс смещения центра масс РН
составляет всего порядка 13% от диаметра ракеты), при большой дли-
не ракеты он может стать причиной соударения ракеты и СН при
старте.
На рис. 6 показаны три варианта расположения РН относительно
СН в конце рассмотренного переходного режима, соответствующие
наиболее вероятному движению и наихудшим сочетаниям кинемати-
ческих параметров на границах областей разброса. Из рисунка следу-
ет, что учет случайного характера воздействия аэродинамических сил
приводит к сложному пространственному движению РН. Видно, что
Рис. 5. Разброс отклонений ракеты (в радианах)
:
а
— по углу тангажа
ϑ
;
б
— по углу рыскания
ψ
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение” 2015. № 1 31

















