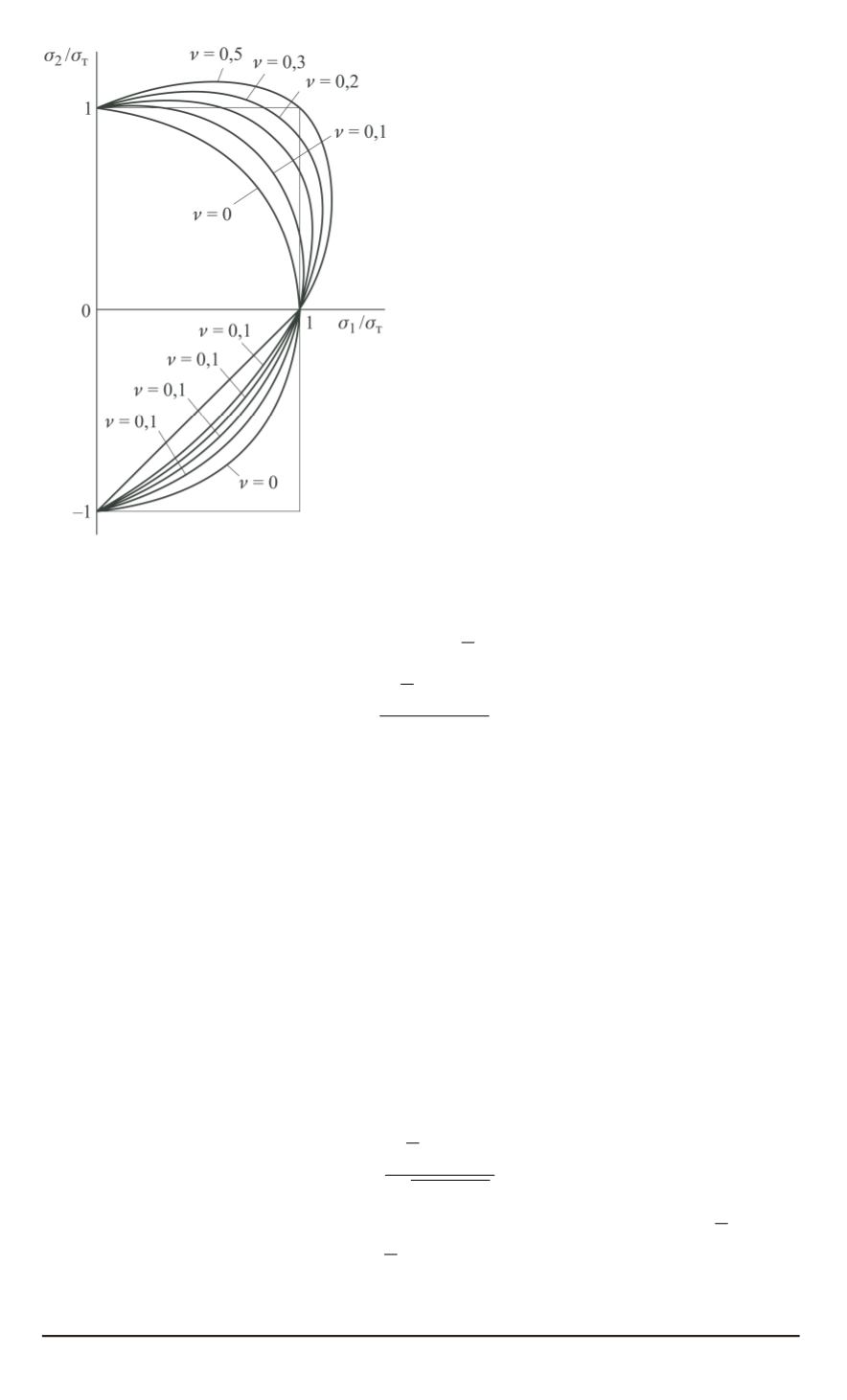
Рис. 1. Условия начала пластическо-
го течения в главных напряжениях
при
σ
33
= 0
Если применить (24) для слу-
чая чистого сдвига, то получим, что
p
i
должно равняться пределу теку-
чести при сдвиге —
τ
т
. Для всех
других видов напряженного состо-
яния в условии начала пластично-
сти будет присутствовать коэффици-
ент Пуассона. Уравнение (24) в ко-
ординатах
σ
11
, σ
22
, σ
33
определя-
ет поверхность второго порядка, а
именно: сфероид с центром в нача-
ле координат, у которого длины двух
главных диаметров
2
d
1
и
2
d
2
равны
между собой и меньше длины тре-
тьего диаметра
2
d
3
, причем третий
диаметр одинаково наклонен по от-
ношению к осям
σ
11
,
σ
22
, σ
33
. Зна-
чения полудлин главных диаметров
d
1
, d
2
, d
3
определяются формулами
d
1
=
d
2
=
√
2
τ
т
,
d
3
=
√
2(1 +
ν
)
(1
−
2
ν
)
τ
т
.
(25)
На рис. 1 графически изображены условия начала пластичности (19),
(20), (24) в координатах
σ
11
, σ
22
(при
σ
33
= 0)
. Прямые линии соот-
ветствуют условию Треска – Сен-Венана (19). При
ν
= 0
,
5
условие
(24) совпадает с условием Хубера –Мизеса (20). При
0
,
5
≥
ν
≥
0
,
3
рассчитанные по (24) кривые располагаются вблизи кривой Хубера –
Мизеса и внутри ее в квадрате I и вне ее в квадрате IV. Общеизвест-
ным является факт, что аналогичным образом относительно кривой
Хубера –Мизеса располагаются точки, полученные из экспериментов,
проведенных на металлах при сложном напряженном состоянии.
Из (24) легко вывести соотношение для параметра
θ
, равного от-
ношению предела текучести при одноосном растяжении
σ
т
к пределу
текучести при сдвиге
τ
т
θ
=
√
2(1 +
ν
)
√
1 + 2
ν
2
.
(26)
Согласно условию Треска – Сен-Венана (19),
θ
равняется
√
2
. Усло-
вие (20) дает для
θ
значение
√
3
. Выражение (26) устанавливает гра-
ницы изменения
θ
в зависимости от коэффициента Пуассона
ν
. При
22 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2014. № 2


