пользованием размера профиля без учета
B
0
при пренебрежении пе
-
ременным характером величины
γ
.
В этом анализе и далее принято
γ
=
−
0
,
03552
·
10
6
.
Найдем значения размера
f
b
L
1
при оговоренных допущениях для ря
-
да значений
¯
b
= (0
,
5; 0
,
6; 0
,
7; 0
,
8; 0
,
9)
при постоянной силе прокатки
P
= 10
МН
.
Для этого необходимо перессчитать зависящие от ширины значе
-
ния вспомогательных величин
ω
,
a
,
e
,
n
.
Новые значения этих величин
приведены в табл
. 4.
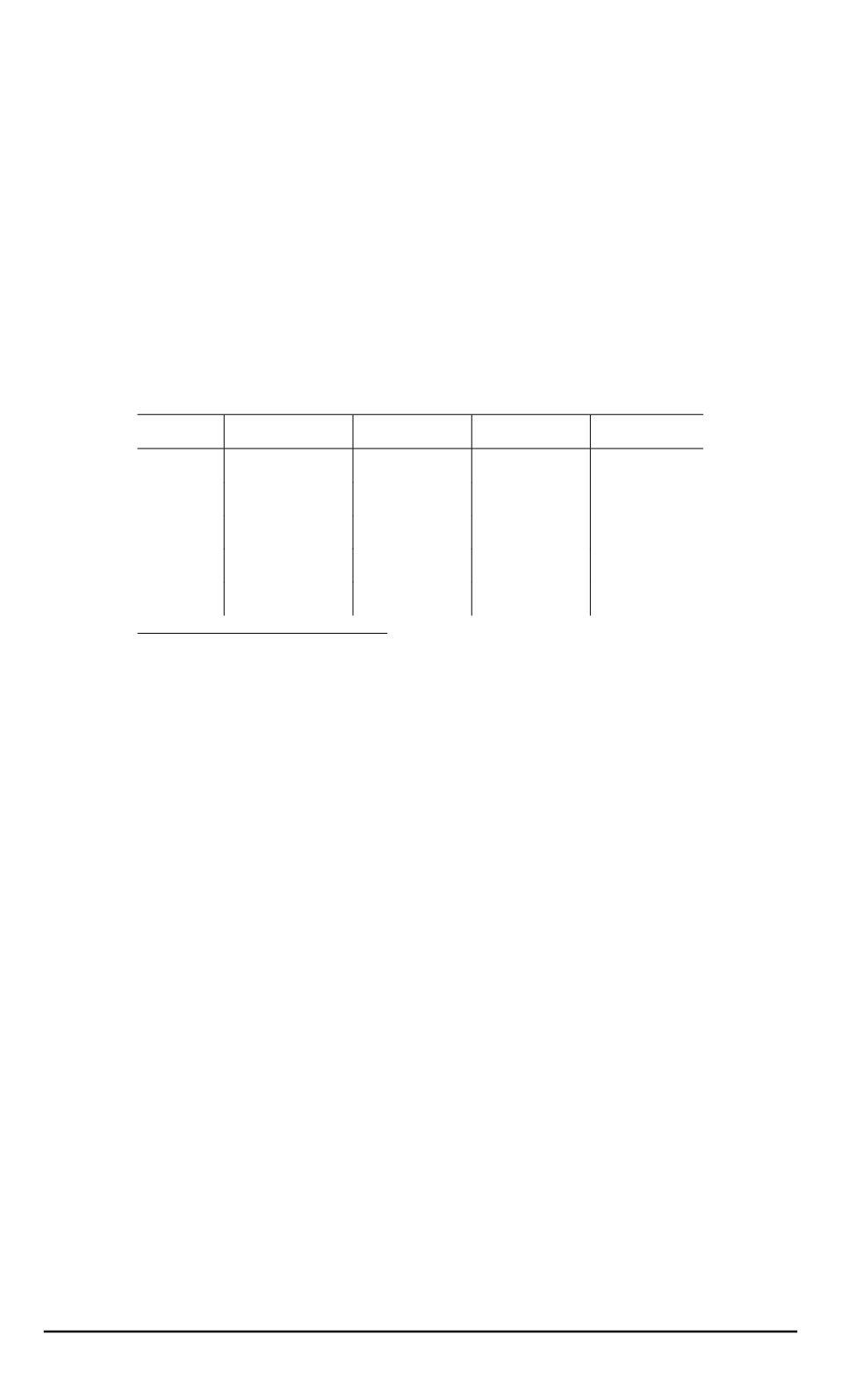
Таблица
4
Перессчитанные значения вспомогательных величин
¯
b
ω
·
10
6
a
·
10
6
e
·
10
6
n
·
10
6
0,5
123,8402 33,5063 24,7377
−
2
,
8093
0,6
∗
119,7050 45,1438 35,7284
−
3
,
9172
0,7
115,1969 57,5925 48,5175
−
4
,
9925
0,8
110,3664 70,5007 62,9759
−
6
,
1228
0,9
105,2647 83,5106 78,9497
−
7
,
2029
∗
Включены прежние значения величин
,
соответствующие
¯
b
= 0
,
6
(
табл
. 2).
По этим данным построены графики вспомогательных величин в
зависимости от ширины
¯
b
(
рис
. 5).
После подстановки в формулу
(8)
значений входящих величин най
-
дены следующие уравнения зависимости
f
b
L
1
=
f
(
ζ
1
; ¯
b
)
:
f
0
,
5
L
1
= (101
,
1348
−
401
,
8853
ζ
1
)
·
10
−
6
при
¯
b
= 0
,
5;
f
0
,
6
L
1
= (73
,
7944
−
417
,
4893
ζ
1
)
·
10
−
6
при
¯
b
= 0
,
6;
f
0
,
7
L
1
= (48
,
7700
−
442
,
6525
ζ
1
)
·
10
−
6
при
¯
b
= 0
,
7;
f
0
,
8
L
1
= (23
,
3598
−
462
,
9789
ζ
1
)
·
10
−
6
при
¯
b
= 0
,
8;
f
0
,
9
L
1
= (
−
1
,
7699
−
483
,
8775
ζ
1
)
·
10
−
6
при
¯
b
= 0
,
9
.
(13)
Поскольку уравнения зависимости
f
b
L
1
=
f
(
ζ
1
; ¯
b
)
при
¯
b
=
const
линейны
,
для их графического представления достаточно рассчитать
размер профиля для двух значений
ζ
1
.
Для контроля правильности
расчетов лучше это выполнить для трех значений
.
В нашем случае
ζ
1
= (0
,
0; 0
,
2; 0
,
4)
.
Рассчитанные по формулам
(13)
значения размера
f
b
L
1
также приве
-
дены в табл
. 3.
ISSN 0236-3941.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Машиностроение
”. 2005.
№
1 109


