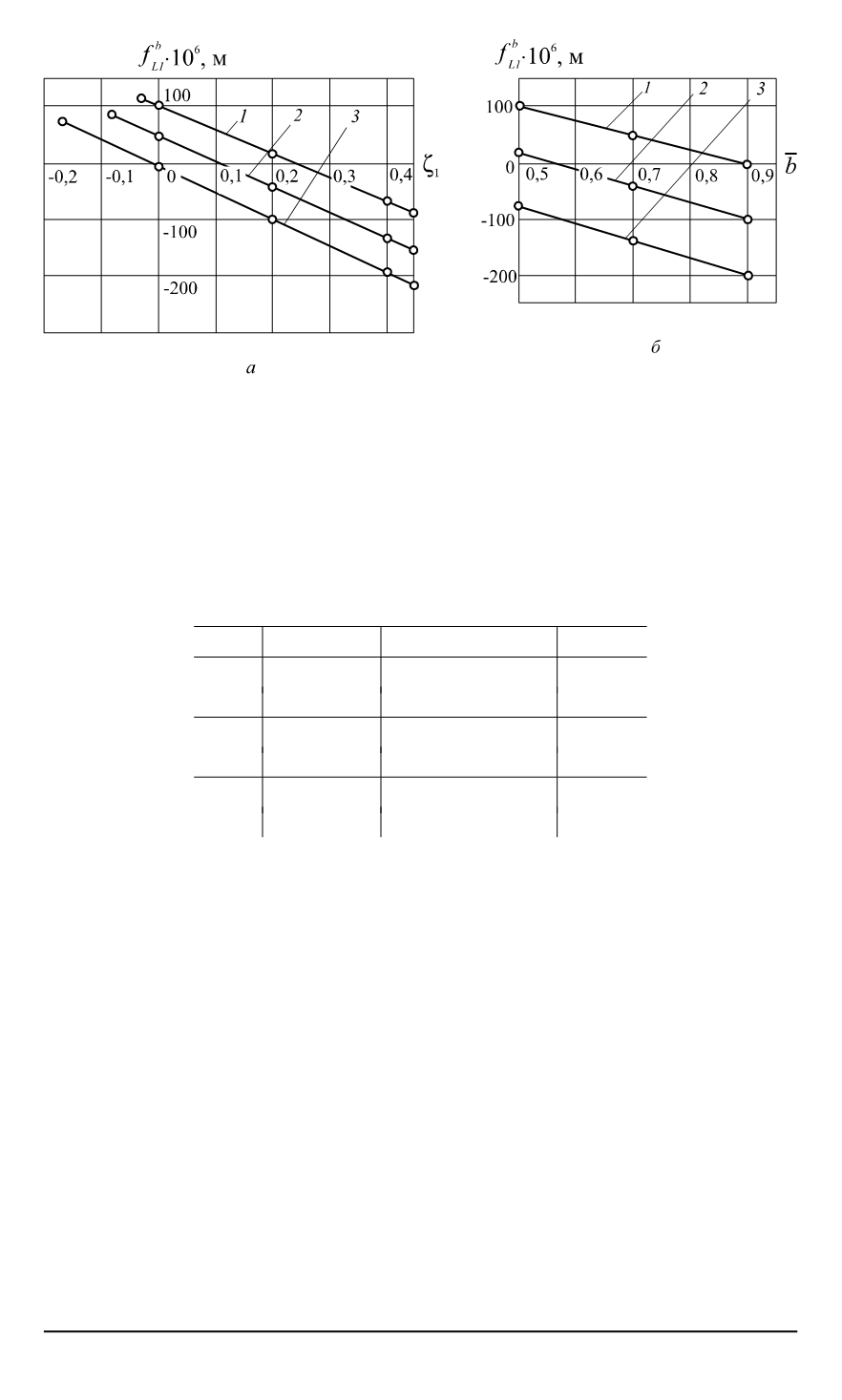
Рис
. 6.
Графики зависимости
f
b
L
1
=
f
(
ζ
1
, b
)
:
1, 2, 3
—
при ширинах полосы
¯
b
= (0
,
5; 0
,
7; 0
,
9
соответственно
) (
a
)
и
1, 2, 3
—
при
значениях величины
ζ
1
= (0
,
0; 0
,
2; 0
,
4
соответственно
) (
б
)
Значения интенсивности изменения зависимости
f
b
L
1
=
f
(
ζ
1
; ¯
b
)
для
разных сил принудительного изгиба
ζ
1
приведены в табл
. 5.
Таблица
5
Изменение параметров валковой системы при
разных значениях силы
ζ
1
ζ
1
∆¯
b
¯ ¯
∂f
b
L
1
/∂
¯
b
¯ ¯
·
10
6
m,
%
0,0 0,5. . . 0,6
273,400
8,1
0,8. . . 0,9
251,297
0,2 0,5. . . 0,6
304,612
3,7
0,8. . . 0,9
293,301
0,4 0,5. . . 0,6
335,820
0,3
0,8. . . 0,9
334,730
В табл
. 5
∆ ¯
b
—
диапазон ширины полосы
,
¯ ¯
∂f
b
L
1
/∂
¯
b
¯ ¯
—
средняя ин
-
тенсивность изменения размера профиля
f
b
L
1
в выделенном диапазо
-
не ширины
;
m
—
процент уменьшения интенсивности при увеличении
ширины от
0,5
до
0,9.
Из полученных данных видно
,
что чем больше сила принудитель
-
ного изгиба
,
тем выше интенсивность изменения профиля
.
Увеличение
ширины
,
наоборот
,
уменьшает эту интенсивность
.
Например
,
при увеличении величины
ζ
1
с
0,2
до
0,4,
средняя ин
-
тенсивность в диапазоне ширины от
0,5
до
0,6
возрастает по модулю
в
1,10
раза
,
а в диапазоне от
0,8
до
0,9 —
в
1,14
раз
.
Таким образом
,
зависимости
f
b
L
1
=
f
(
ζ
1
; ¯
b
)
при
ζ
1
=
const
практически можно считать
линейными
.
Анализ влияния профилировки опорных валков
.
Это влияние
проанализировано для
P
= 10
,
b
= 0
,
7
и
γ
=
−
0
,
03552
·
10
6
при
следующих значениях размера
f
L
2
= (
−
200;
−
100; 0; 100; 200)
·
10
−
6
.
ISSN 0236-3941.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Машиностроение
”. 2005.
№
1 111


