После подстановки в выражение
(8)
известных значений входящих
величин и поочередно значений
f
L
2
из ряда были получены следующие
уравнения зависимости
f
f
L
2
L
1
=
f
(
ζ
1
;
f
L
2
)
:
f
f
L
2
L
1
= (23
,
6684
−
442
,
6525
ζ
1
)
·
10
−
6
при
f
L
2
·
10
6
= 200;
f
f
L
2
L
1
= (50
,
2431
−
442
,
6525
ζ
1
)
·
10
−
6
при
f
L
2
·
10
6
= 100;
f
f
L
2
L
1
= (76
,
8179
−
442
,
6525
ζ
1
)
·
10
−
6
при
f
L
2
·
10
6
= 0;
f
f
L
2
L
1
= (103
,
3927
−
442
,
6525
ζ
1
)
·
10
−
6
при
f
L
2
·
10
6
=
−
100;
f
f
L
2
L
1
= (129
,
9286
−
442
,
6525
ζ
1
)
·
10
−
6
при
f
L
2
·
10
6
=
−
200
.
(14)
Определим
f
f
L
2
L
1
для трех значений
ζ
1
= (0
,
0; 0
,
2; 0
,
4)
.
Полученные значения
f
f
L
2
L
1
для всего ряда
f
L
2
сведены в табл
. 3.
Ис
-
пользуя уравнения
(9)
и
(14)
уточним интервалы изменения
ζ
1
по мето
-
дике
,
применяемой при анализе влияния ширины полосы
.
Результаты
приведены в табл
. 3.
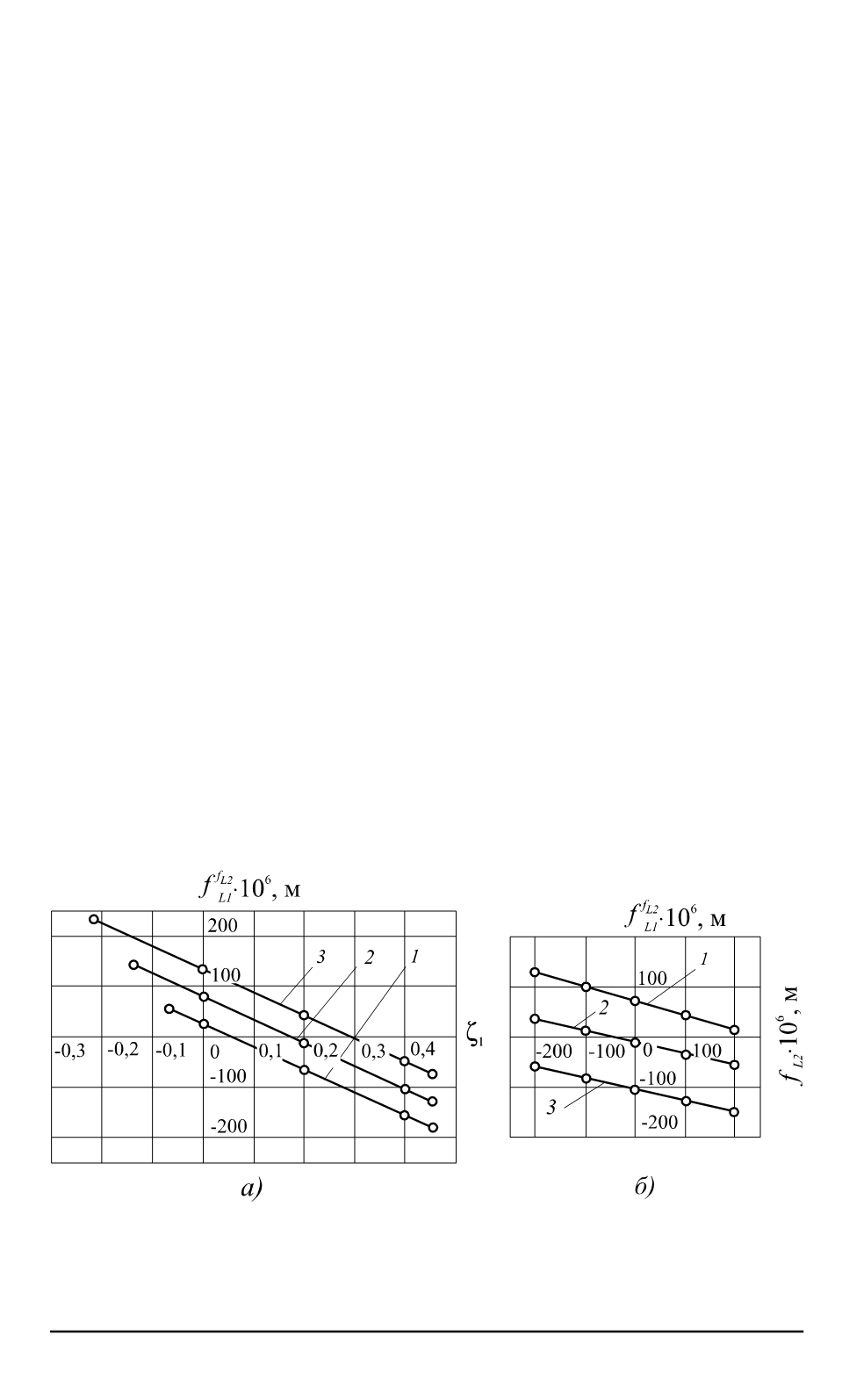
По полученным данным построены графики уравнений
(14)
с изме
-
нением
ζ
1
для трех значений профилировки
f
L
2
= (200; 0
,
0;
−
200)
×
×
10
−
6
,
представленные на рис
. 7,
а
.
Эти графики линейные с одина
-
ковым углом наклона
(
∂f
f
L
2
L
1
/∂ζ
1
=
−
442
,
6525
·
10
−
6
)
.
С уменьшением
размера профиля
f
L
2
интервал
ζ
1
равномерно расширяется за счет ниж
-
него предела
.
На рис
. 7,
б
приведены графики зависимости
f
L
2
L
1
=
f
(
ζ
1
;
f
L
2
)
при
f
L
2
=
var
для трех значений величины
ζ
1
= (0
,
0; 0
,
2; 0
,
4)
.
Графи
-
ки также линейные с одним и тем же углом наклона
(
∂f
f
L
2
L
1
/∂f
L
2
=
Рис
. 7.
Графики зависимости
f
f
L
2
L
1
=
f
(
ζ
1
, f
L
2
)
:
1, 2, 3
—
соответственно при значениях величины
f
L
2
= (200; 0
,
0;
−
200)
·
10
−
6
(
a
)
и
1, 2, 3
—
при значениях величины
ζ
1
= (0
,
0; 0
,
2; 0
,
4
соответственно
) (
б
)
112 ISSN 0236-3941.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Машиностроение
”. 2005.
№
1


