Используя аналогичный подход
,
удается получить сгущение вблизи
двух границ отрезка
[5]:
η
j
=
1
2
½
1 +
ln (1 +
P
¯
η
j
)
ln (1 +
P
)
−
ln [1 +
Q
(1
−
¯
η
j
)]
ln (1 +
Q
)
¾
.
Имеются также формулы для сгущения узлов сетки в окрестности про
-
межуточной точки отрезка
[6].
Весьма простые формулы растяжения основаны на тригонометри
-
ческих соотношениях
.
Например
,
сгущение сетки вблизи обеих границ
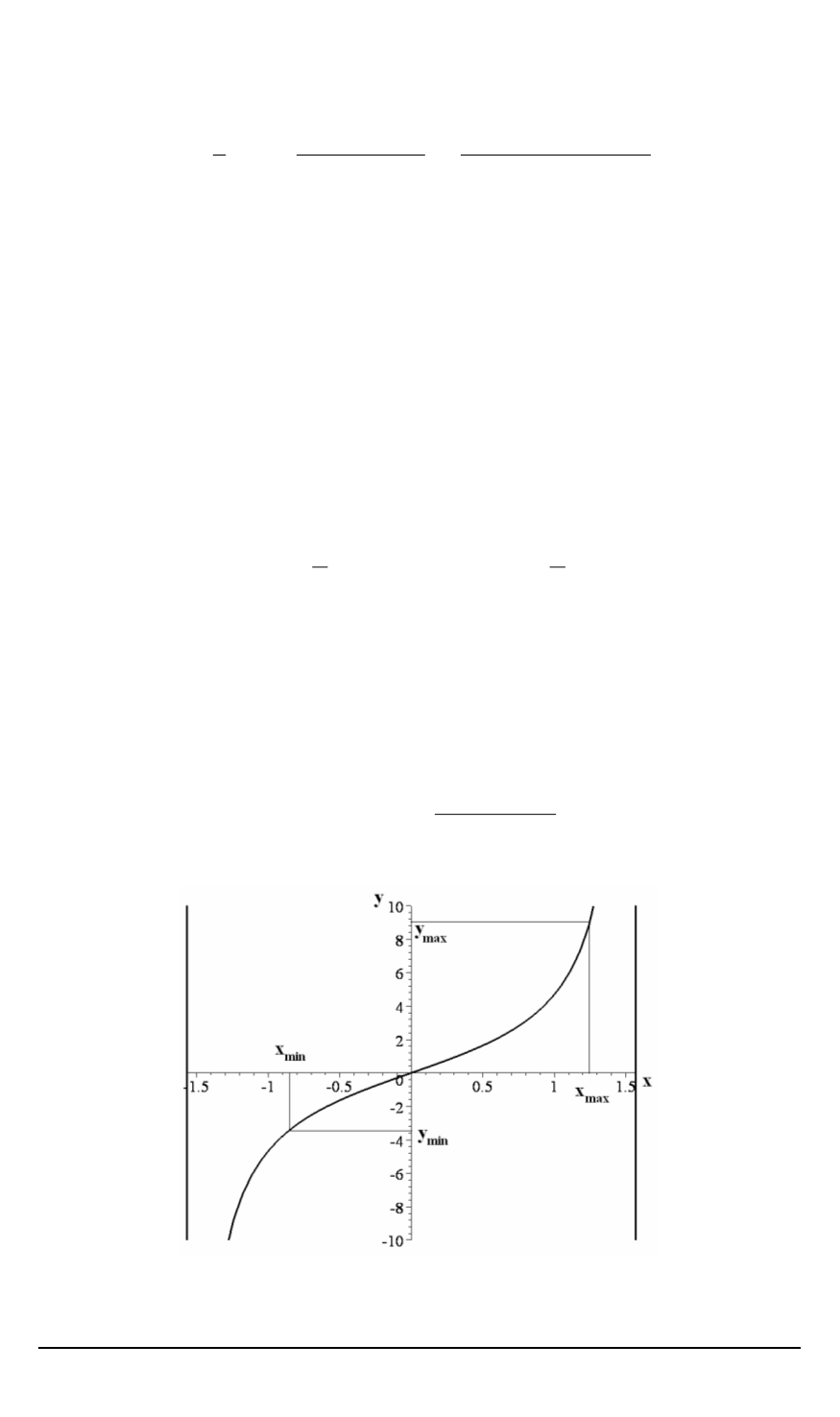
отрезка или в его центральной части позволяет получить формула вида
y
=
tg(
βx
)
,
где
β
—
параметр сгущения сетки
.
Рассмотрим построение сетки со сгущениями вблизи границ отрез
-
ка единичной длины
[
s
A
= 0
, s
B
= 1]
.
Пусть
x
min
=
−
π
2
+
ε
1
и
x
max
= +
π
2
−
ε
2
,
где величины
ε
1
,
2
6
= 0
так же
,
как и параметр сгущения сетки
β
,
позво
-
ляют регулировать степень неоднородности сетки вблизи границ
A
и
B
(
рис
. 5).
Если
ε
1
=
ε
2
,
то сгущение сетки вблизи обеих границ одина
-
ково
e,
если
ε
1
6
=
ε
2
—
разное
.
В рассматриваемом случае однородная сетка
¯
ω
j
=
½
y
j
=
y
min
+ (
j
−
1) ¯
h
; ¯
h
=
y
max
−
y
min
NJ
−
1
;
j
= 1
,
2
, . . . , NJ
¾
Рис
. 5.
К построению неоднородной расчетной сетки с использованием тригоно
-
метрических функций
ISSN 0236-3941.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Машиностроение
”. 2004.
№
2 35


