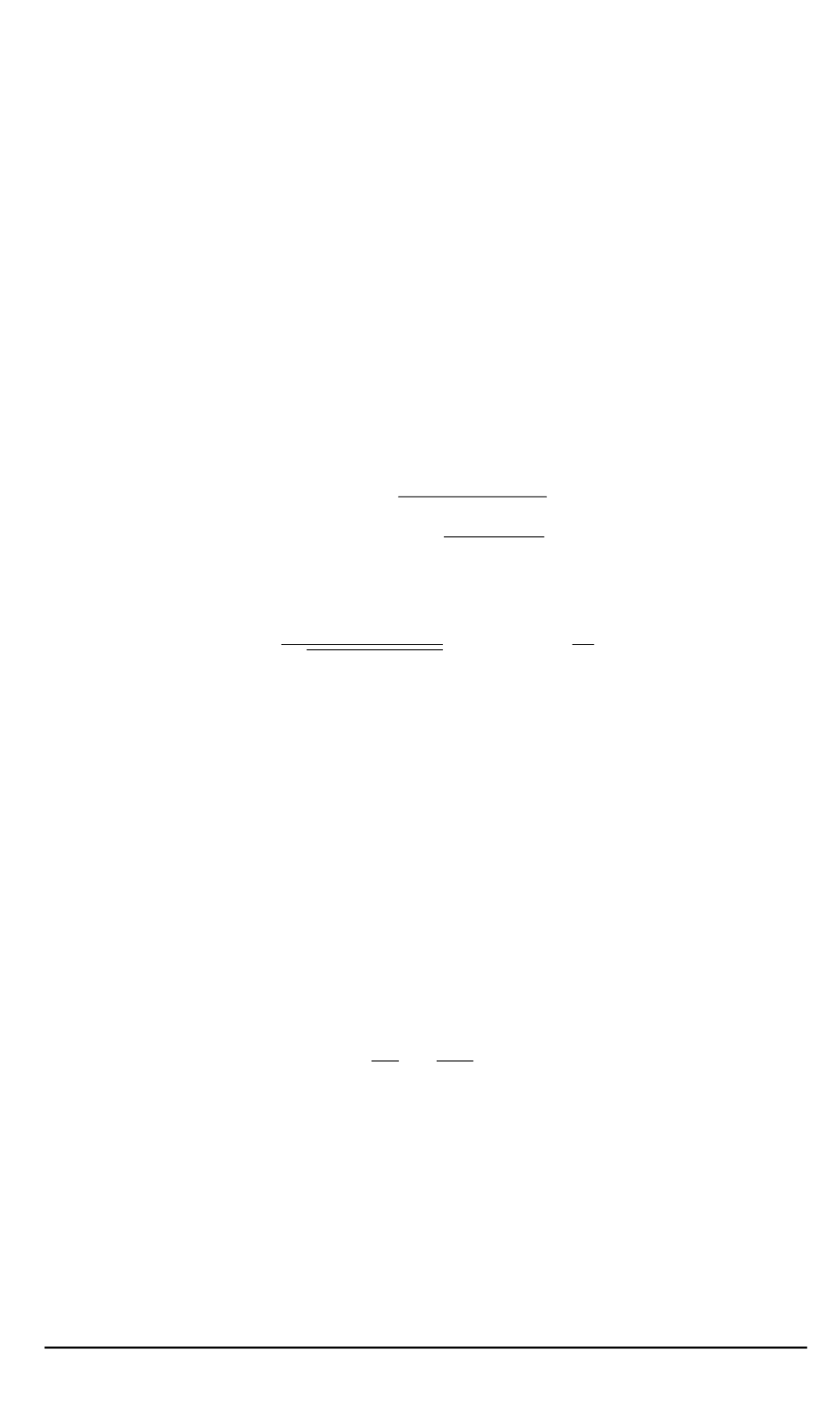
Для построения сетки блока №
2
применен аналитический метод
.
На участке
A
2
B
2
расположение узлов сетки считается заданным
,
так
как эта конфигурация уже определена для блока №
1.
На участках по
-
верхности
B
2
C
2
и
C
2
D
2
расположение точек задано в соответствии с
функцией сжатия
S
BC
и
S
CD
(
подробнее функции сжатия обсуждаются
ниже
).
Кроме того
,
из общего числа точек
NJ
2
,
заданных для границ
A
2
B
2
C
2
D
2
и
F
2
E
2
,
число
NI
1
определено для блока №
1
.
Оставшие
-
ся
(
NJ
2
−
NI
1 + 1
)
точки распределяются на участках
B
2
C
2
и
C
2
D
2
в зависимости от геометрии задней поверхности КА
.
Таким образом
,
в рассматриваемом алгоритме построения расчетной сетки блока №
2
изначально считаются заданными координаты точек
(
r
j
, z
j
)
на границе
A
2
B
2
C
2
D
2
.
Из каждой точки
(
r
j
, z
j
)
до границы
E
2
F
2
проводится дуга эллипса
,
вычисляемая по следующим формулам
:
r
=
H
j
s
1
−
(
z
−
L
0
)
2
L
2
j
,
(
3
)
где
L
j
=
L
0
−
z
j
q
1
−
¡
r
2
j
±
H
2
j
¢
,
H
j
=
r
j
r
1
R
0
.
Соотношение
(3)
задает эллипс
,
проходящий через точки
(
r
j
, z
j
)
и
(
H
j
, L
0
) (
см
.
рис
. 1,
б
).
Заметим
,
что величину
H
j
можно выбирать по
-
другому
,
однако
,
если окажется
,
что
H
j
< z
j
,
то указанный алгоритм приведет к ошиб
-
ке
.
В первой расчетной области используется алгоритм алгебраических
отображений
,
подробно изложенный в работе
[4].
Помимо расчетной сетки
,
ограниченной эллиптической поверхно
-
стью
,
представляет интерес класс расчетных сеток
,
ограниченных сте
-
пенной зависимостью вида
z
L
0
=
r
m
R
m
0
,
(
4
)
где
m
>
2
.
Как уже отмечалось ранее
,
уравнение любого луча
,
находящегося
внутри расчетной области
,
определяется формулой
(2),
поэтому для
определения координат точек пересечения луча с поверхностью необ
-
ходимо решить систему уравнений
(2)
и
(4),
дополненную уравнением
плоскости
z
=
L
0
.
30 ISSN 0236-3941.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Машиностроение
”. 2004.
№
2