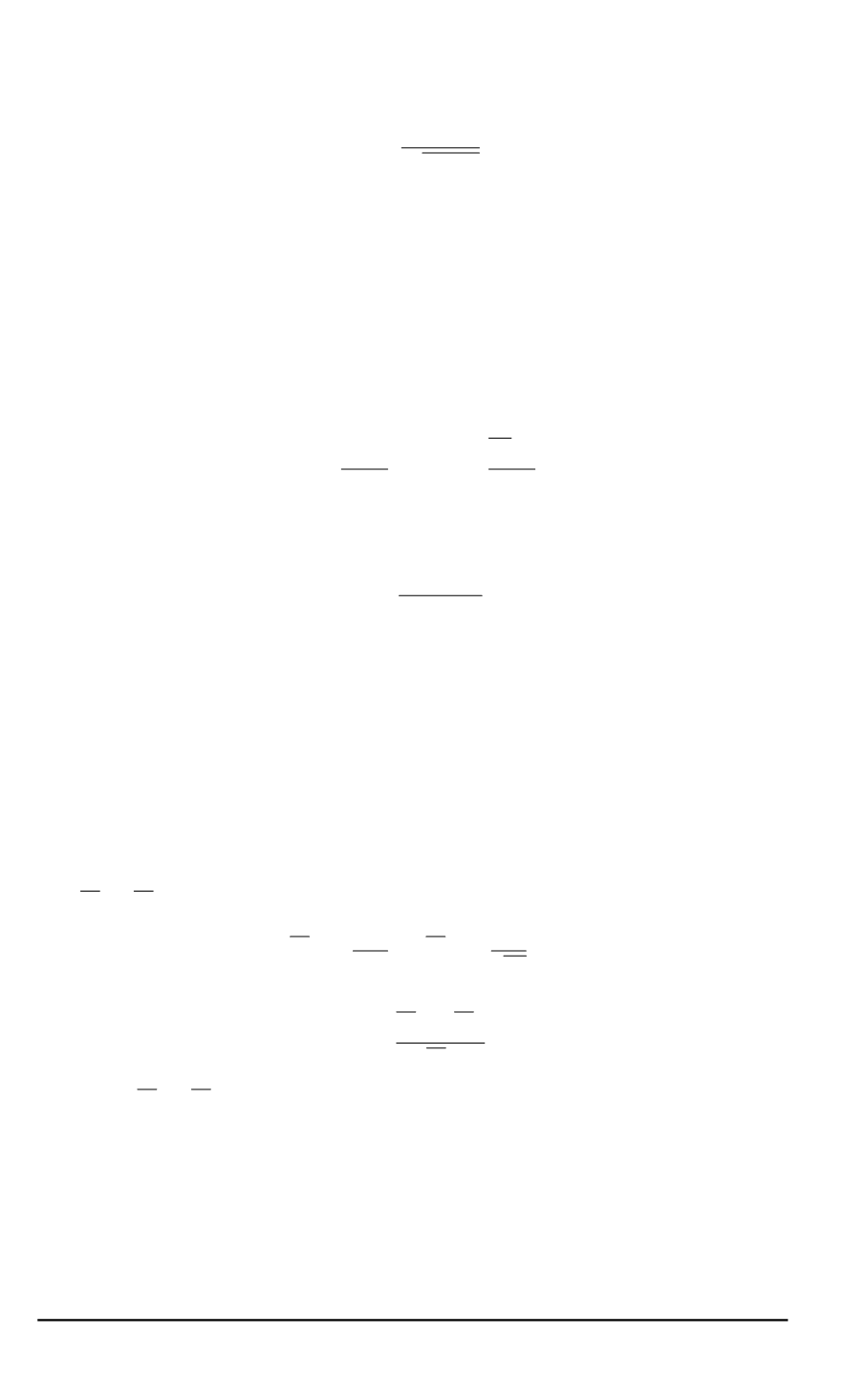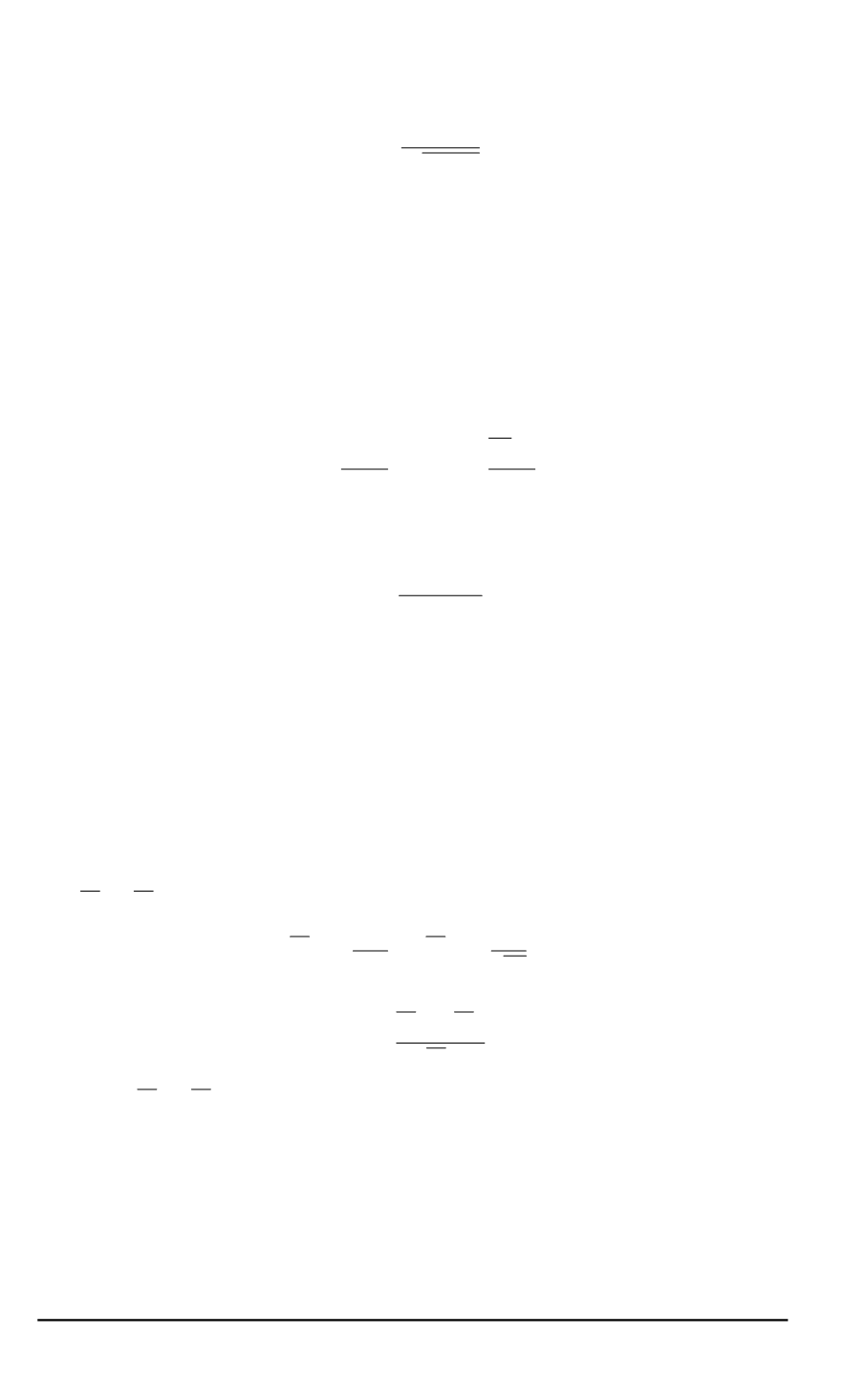
Следовательно
,
коэффициент электромеханической связи можно
определить по формуле
k
эс
=
U
eel
√
U
e
U
el
.
Эта зависимость была предложена в работе
[8].
Ее целесообразно
использовать для теоретического анализа коэффициента
k
эс
.
Рассмотрим другие варианты энергетического способа определения
коэффициента электромеханической связи
.
Для одного и того же пе
-
ремещения
u
определим энергию упругого деформирования пружины
для замкнутых и разомкнутых пластин
.
Обозначим эти энергии соот
-
ветственно символами
U
з
и
U
p
,
тогда
U
з
=
Ku
2
2
;
U
p
=
Ku
2
2
.
Отсюда вытекает следующая зависимость
:
k
2
эс
=
U
p
−
U
з
U
p
.
Такой способ определения коэффициента электромеханической связи
рассматривается в работах
[10, 11].
При этом разность
U
р
−
U
з
назы
-
вают энергией
,
способной к обращению
.
При неизменном перемеще
-
нии
u
эта энергия затрачивается на наведение электрических зарядов
на пластинах конденсатора
.
Можно поступить иначе
.
Для одной и той же силы
F
определим
энергию упругого деформирования пружины в случае замкнутых и ра
-
зомкнутых пластин
.
Введем обозначения для соответствующих энер
-
гий
U
з
и
U
p
,
тогда
U
з
=
F
2
2
K
;
U
p
=
F
2
2
K
,
откуда
k
2
эс
=
U
з
−
U
p
U
з
.
Разность
U
з
−
U
p
также можно рассматривать как энергию обращения
.
При неизменной силе
F
на эту величину изменяется энергия упругого
деформирования пружины при размыкании первоначально замкнутых
пластин
.
Эта энергия затрачивается на наведение зарядов
.
Предложен
-
ные способы определения коэффициента электромеханической связи
могут быть полезными при теоретическом анализе характеристик ма
-
териалов
,
а также устройств
,
работающих на основе пьезоэффекта
.
ISSN 0236-3941.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. "
Машиностроение
". 2003.
№
3 17