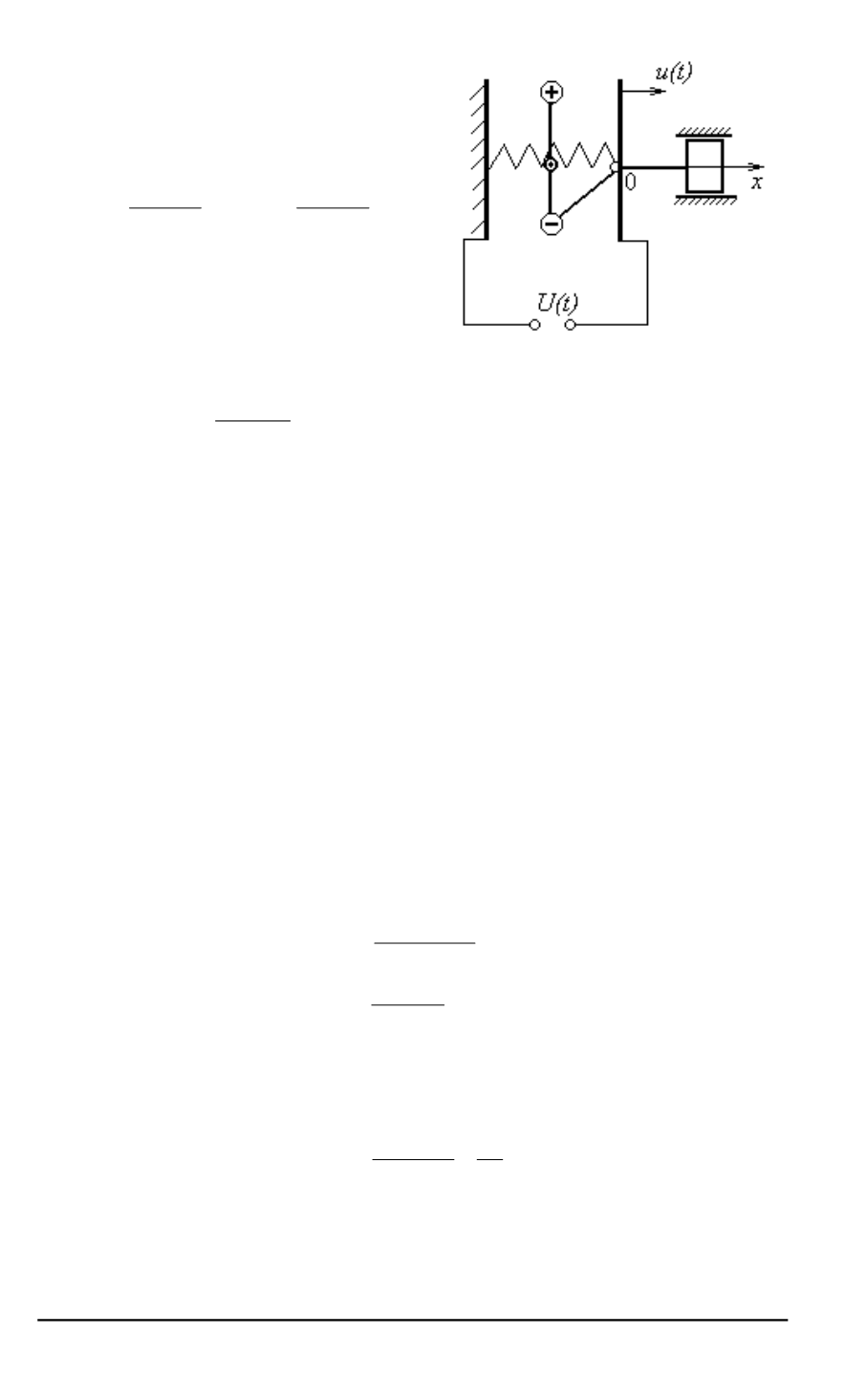
Рис
. 4.
Схема нагружения электроме
-
ханической системы при определении
коэффициента электромеханической
связи
При этом равенства
(14)
для ча
-
стот собственных колебаний элек
-
тромеханической системы упроща
-
ются и принимают вид
p
2
1
=
ω
2
10
1 +
k
эс
;
p
2
2
=
ω
2
01
1
−
k
эс
.
Отсюда можно получить еще од
-
ну формулу для расчета коэффици
-
ента электромеханической связи
,
а
именно
:
k
эс
=
p
2
2
−
p
2
1
p
2
2
+
p
2
1
.
Таким образом
,
в общем случае
при динамическом способе определения коэффициента электромеха
-
нической связи следует учитывать характеристики электрической це
-
пи
,
в частности ее индуктивность
.
Пьезоэлектрический гаситель колебаний
.
С помощью предло
-
женной электромеханической модели пьезоэлектрика можно каче
-
ственно объяснить принципы функционирования пьезоэлектрических
устройств
.
Рассмотрим пассивный пьезоэлектрический гаситель ко
-
лебаний
,
который может быть использован в авиационной технике
,
в прецизионных космических конструкциях
[4].
Одна из возможных
принципиальных схем такого устройства показана на рис
. 5,
а
.
К телу
массой
m
приложена возбуждающая сила
P
(
t
)
.
Электромеханическая
модель включена в электрический контур
,
содержащий катушку с ин
-
дуктивностью
L
.
Полагая в формулах
(16)
U
0
= 0
,
получим
u
0
=
(
ω
2
2
−
β
2
)
m
∆
P
0
;
q
0
=
dω
2
01
ω
2
2
∆
P
0
.
(
21
)
Видно
,
что при
k
эс
= 0
,
т
.
е
.
при
d
= 0
,
амплитуда установившихся
колебаний
u
0
определяется по формуле
u
0
=
ω
2
1
ω
2
1
−
β
2
·
P
0
K
.
(22)
Эта величина соответствует амплитуде колебаний механической систе
-
мы с одной степенью свободы с частотой собственных колебаний
ω
1
=
=
ω
01
.
При этом заряд на пластинах не индуцируется
.
ISSN 0236-3941.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. "
Машиностроение
". 2003.
№
3 23


