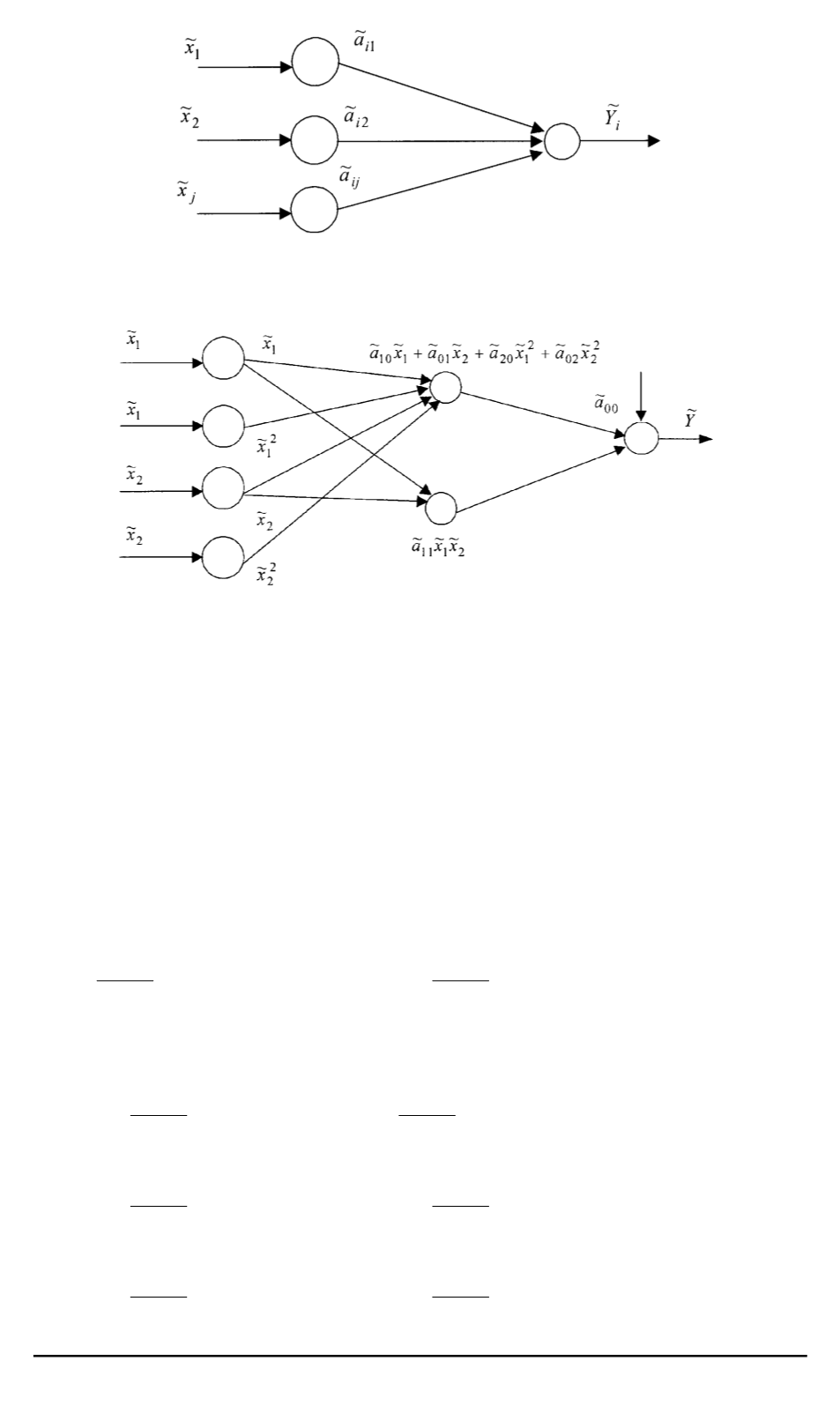
Рис. 4. Структура нейронной сети для многомерного линейного уравнения ре-
грессии
Рис. 5. Схема нейронной сети для уравнения регрессии второго порядка
Следует отметить, что при отрицательных значениях параметра
˜
a
rs
(
˜
a
rs
<
0
) формулы, которые включают в себя параметры
˜
a
rs
, в урав-
нении (3), и коррекция данного параметра в выражениях (4) будут
изменять свою формулу.
Например, допустим, что
˜
a
rs
<
0
, тогда формула вычисления чет-
вертого выражения, которая включает в себя
˜
a
rs
, в уравнении (3), будет
иметь следующий вид:
y
41
=
a
111
x
12
x
22
;
y
42
=
a
112
x
12
x
21
, а формулы
коррекции —
∂E
1
∂a
111
=
k
X
j
=1
(
y
j
1
−
t
j
1
)
x
12
x
22
;
∂E
2
∂a
112
=
k
X
j
=1
(
y
j
2
−
t
j
2
)
x
11
x
21
.
Для значения
α
= 1
получим
∂E
3
∂a
003
=
k
X
j
=1
(
y
j
3
−
t
j
3
);
∂E
3
∂a
113
=
k
X
j
=1
(
y
j
3
−
t
j
3
)
x
13
x
23
;
∂E
3
∂a
103
=
k
X
j
=1
(
y
j
3
−
t
j
3
)
x
13
;
∂E
3
∂a
203
=
k
X
j
=1
(
y
j
3
−
t
j
3
)
x
2
13
;
∂E
3
∂a
013
=
k
X
j
=1
(
y
j
3
−
t
j
3
)
x
23
;
∂E
3
∂a
023
=
k
X
j
=1
(
y
j
3
−
t
j
3
)
x
2
23
.
(5)
104 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2006. № 2


