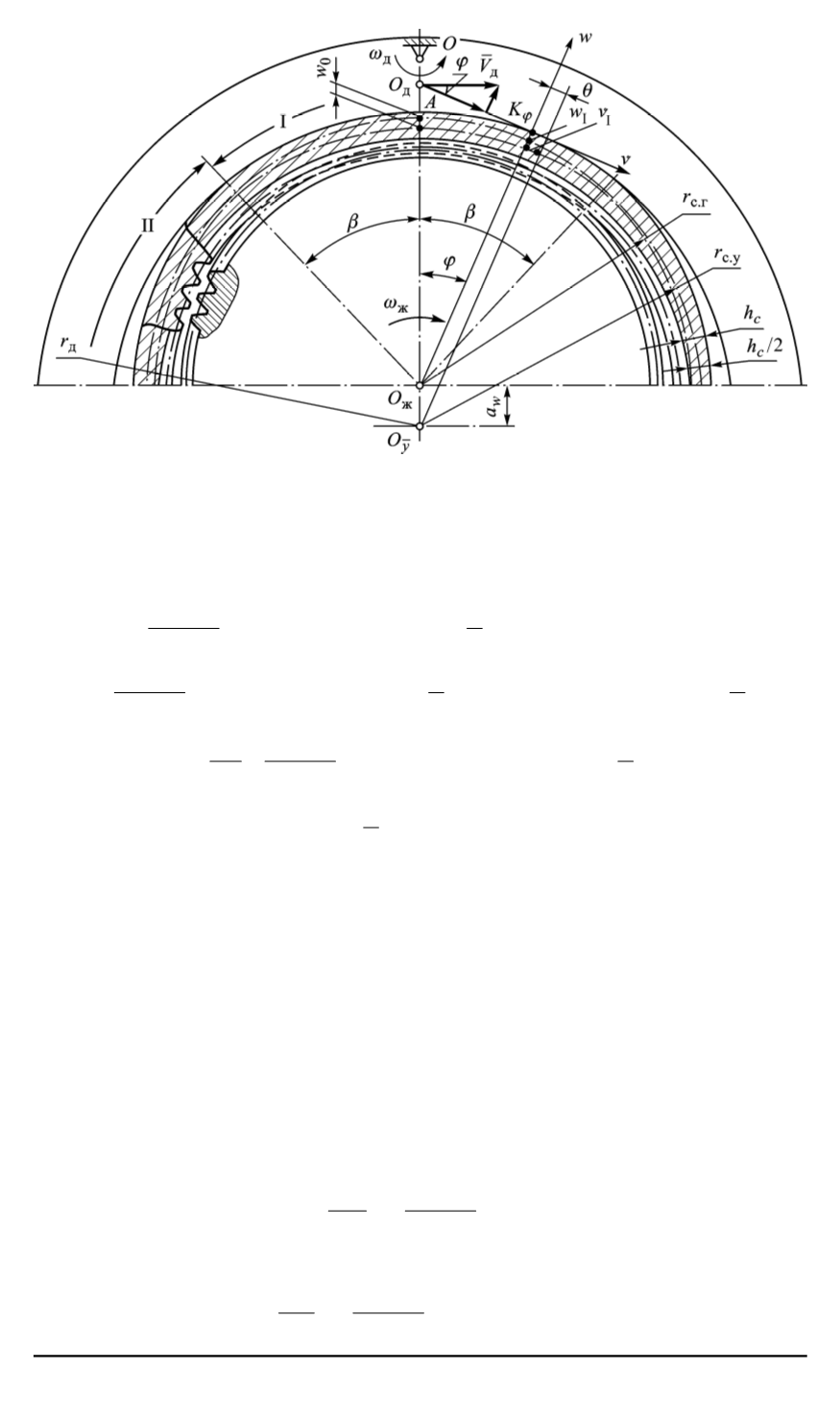
Рис. 3. Расчетная схема зацепления в ВЗП внешнего деформирования
— для участка I (
0
6
ϕ
6
β
), где гибкое колесо принудительно дефор-
мируется генератором волн по дугам постоянного радиуса;
ω
II
=
−
w
0
A
−
Б
h
1
−
sin
2
β
sin
ϕ
+
π
2
−
ϕ
cos
ϕ
−
2 sin
β
−
Б
i
,
v
II
=
−
w
0
A
−
Б
h
−
(2+sin
2
β
) cos
ϕ
+
π
2
−
ϕ
sin
ϕ
+ 2 sin
β
+
Б
π
2
−
ϕ
i
,
θ
II
=
−
w
0
r
с.г
∙
1
A
−
Б
h
2 cos
ϕ
−
(2 sin
β
+
Б
)
π
2
−
ϕ
i
— для участка II
β < ϕ
6
π
2
, где
β
— угловая координата участ-
ка постоянной кривизны;
ϕ
— угловая координата рассматриваемого
сечения, отсчитываемая от малой оси деформации;
r
с.г
— радиус кри-
визны срединной линии недеформированного гибкого колеса;
w
0
—
радиальное перемещение по малой оси;
w, v
и
θ
— радиальные, тан-
генциальные и угловые перемещения соответственно.
Продифференцируем по времени аналитические выражения соста-
вляющих перемещений. Поскольку изменение угла
ϕ
пропорциональ-
но скорости вращения деформированной средней кривой, то можно
записать
ϕ
=
−
ω
ж
t
.
Для первого участка
v
w
1
=
dw
I
dt
=
w
0
A
A
−
Б
ω
ж
sin
ω
ж
t
— радиальная скорость;
v
ϑ
I
=
dv
1
dt
=
w
0
A
−
Б
ω
ж
(
A
cos
ω t
−
Б
)
6 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2011. № 4


