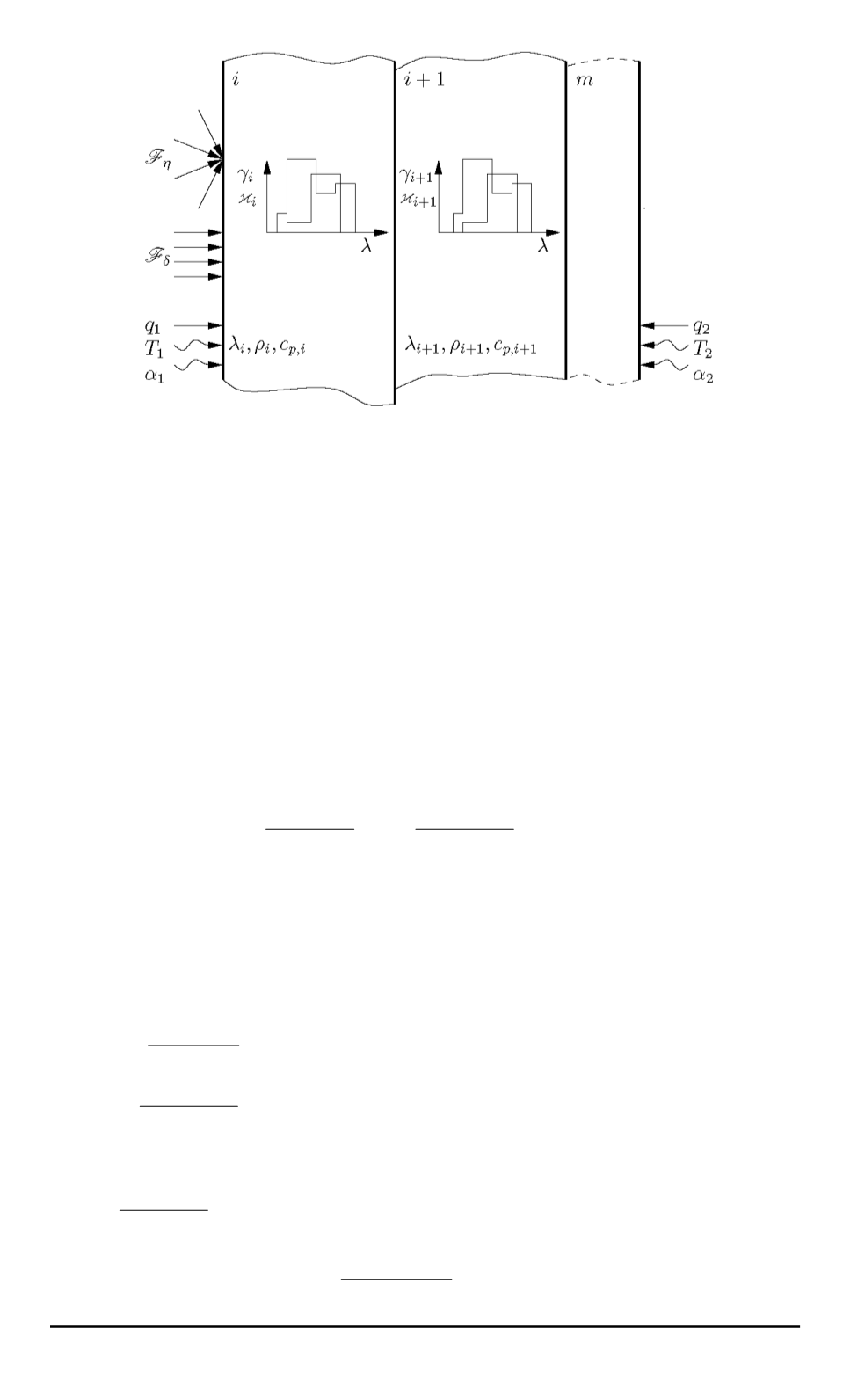
Рис. 3. Физическая модель многослойной системы и внешнего теплового
нагружения
пловыделения произвольной природы, например, при химических ре-
акциях или поглощении ионизирующего излучения. В основу предла-
гаемого метода положено аналитическое решение уравнения переноса
излучения методом моментов [32] для системы произвольного числа
рассеивающих слоев с учетом собственного излучения [33] и решение
уравнения энергии методом конечных элементов.
Модель теплопередачи.
Представим систему конечным числом
слоев с заданными оптическими и теплофизическими свойствами
(рис. 3). Температурное поле в каждом
i
-м слое описывается диффе-
ренциальным уравнением теплопроводности
c
p,i
ρ
i
∂T
i
(
x, t
)
∂t
= Λ
i
∂
2
T
i
(
x, t
)
∂x
2
+
q
v,i
(
x, t
)
,
(4)
а
m
уравнений (по числу слоев) образуют систему, которую необхо-
димо дополнить начальными условиями
T
i
(0
, x
) =
T
i,
0
(
x
)
(5)
и граничными условиями
Λ
1
∂T
1
(
x, t
)
∂x
|
x
=0
=
F
1
+
q
1
+
α
1
[
T
1
(0
, t
)
−
T
ср, 1
]
−
σ
0
T
4
1 1
;
(6)
−
Λ
m
∂T
m
(
x, t
)
∂x
|
x
=
h
=
q
2
+
α
2
[
T
m
(
h, t
)
−
T
ср, 2
]
−
σ
0
T
4
2
m
,
(7)
а также условиями сопряжения на границах слоев
Λ
i
∂T
i
(
x, t
)
∂x
−
σ
0
T
4
i i
x
=
h
+
q
0
r,i
+1
i
=
= Λ
i
+1
∂T
i
+1
(
x, t
)
∂x
−
σ
0
T
4
i
+1
i
+1
x
=0
+
q
r,i i
+1
,
(8)
16 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2008. № 1


