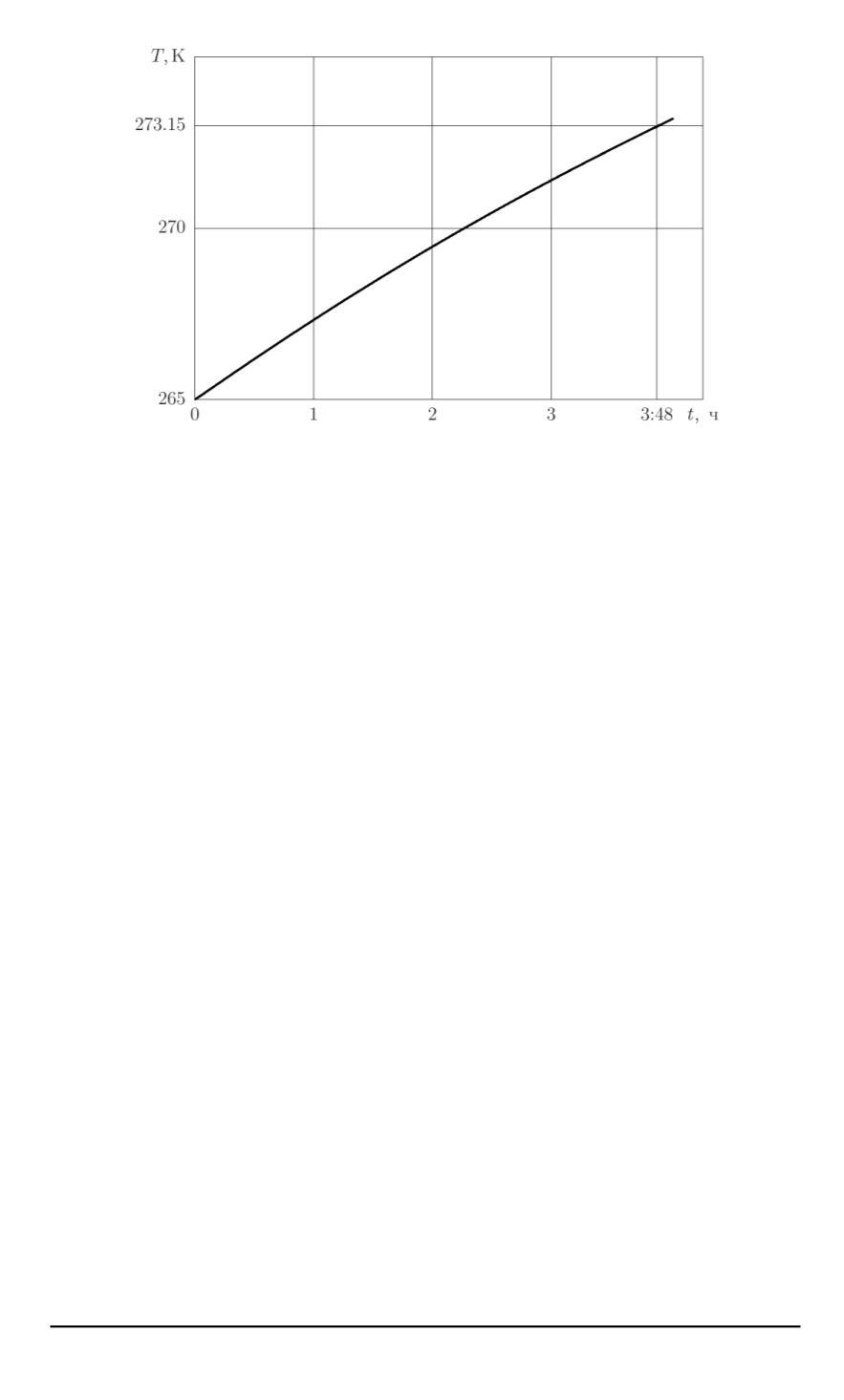
Рис. 7. Зависимость температуры в точке максимального энерговыделения в
слое снега от времени нагрева
с поверхностью земли со степенью черноты
= 1
и температуру
−
8
◦
C, т.е. предполагается тепловое равновесие со снежным покро-
вом и полное поглощение излучения поверхностью земли. Тепло- и
оптико-физические свойства снега (фирна) приняты следующими [29]:
плотность
ρ
= 300
кг/м
3
; теплоемкость
C
= 2100
Дж/(кг
∙
K); тепло-
проводность
λ
= 0
,
36
Вт/(м
∙
K); коэффициент поглощения
κ
= 1
м
−
1
;
удельный коэффициент рассеяния
γ
= 10
. При указанных оптических
свойствах с учетом направленности излучения Солнца максимум объ-
емного тепловыделения [37] имеет место на глубине 0,15 м; на рис. 7
приведен график зависимости температуры в этой точке от времени
нагрева, из которого следует, что температура плавления снега до-
стигается через 14000 с (3 ч 48 мин) с момента начала воздействия
излучения Солнца, что соответствует полученным эксперименталь-
ным данным.
Отметим, что проблема таяния снежно-ледяных массивов во вну-
тренних слоях исключительно важна с точки зрения прогнозирования
схода лавин, так как образование водяного слоя служит причиной на-
рушения сплошности (разрыв) массива и облегчает сход (скольжение)
внешнего слоя, т.е. образование лавины.
Выводы.
Дана общая постановка, приведены физическая и мате-
матическая модели задачи радиационно-кондуктивного теплообмена
в многослойной рассеивающей среде и метод ее решения. Приведе-
ны примеры, иллюстрирующие практическую важность рассмотрен-
ной задачи. Программная реализация задачи на языке C++ доведена
до возможности ее использования при решении широкого круга задач
радиационно-кондуктивного теплообмена в различных областях науки
и техники.
26 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2008. № 1


