слоя в этом же направлении, в общем случае переменный по тол-
щине этого слоя. Если аналогично формуле для
λ
∗
⊥
непрерывное
изменение
λ
∗
представить зависимостью
λ
∗
(
r
) =
λ
∗
exp(
a
∗
r
)
, удо-
влетворяющей условиям
λ
◦
=
λ
∗
exp(
a
∗
r
0
)
и
λ
m
=
λ
∗
exp(
a
∗
r
1
)
, где
a
∗
r
1
=
−
ln ¯
λ /
(1
−
r
0
/r
1
)
,
λ
∗
=
λ
m
exp(
a
∗
r
1
)
и
¯
λ
=
λ
◦
/λ
m
, то вместо
равенства (13) можно записать:
λ
=
λ
λ
m
= 1
−
C
V
+
C
V
r
2
0
r
2
1
¯
λ
+ 2
C
V
a
∗
r
1
−
1
−
(
a
∗
r
0
−
1) ¯
λ
(
a
∗
r
1
)
2
.
(14)
При отсутствии промежуточного слоя (
r
0
→
r
1
и
a
∗
→ ∞
) формула
(14) переходит в равенство
λ
◦
= 1
−
C
V
+
C
V
¯
λ
, из которого следует,
что
λ
◦
< λ
при
¯
λ <
1
и
λ
◦
> λ
при
¯
λ >
1
.
Построение двусторонних оценок.
Для оценки возможной по-
грешности формул (11) и (14) используем двойственную вариацион-
ную формулировку задачи стационарной теплопроводности [12,13],
позволяющую получить двусторонние оценки эффективных коэффи-
циентов теплопроводности рассматриваемого композита. Область
V
,
содержащую представительный элемент в виде половины составной
частицы радиусом
r
m
, выберем в форме прямоугольного параллелепи-
педа длиной
L r
m
и высотой
H r
m
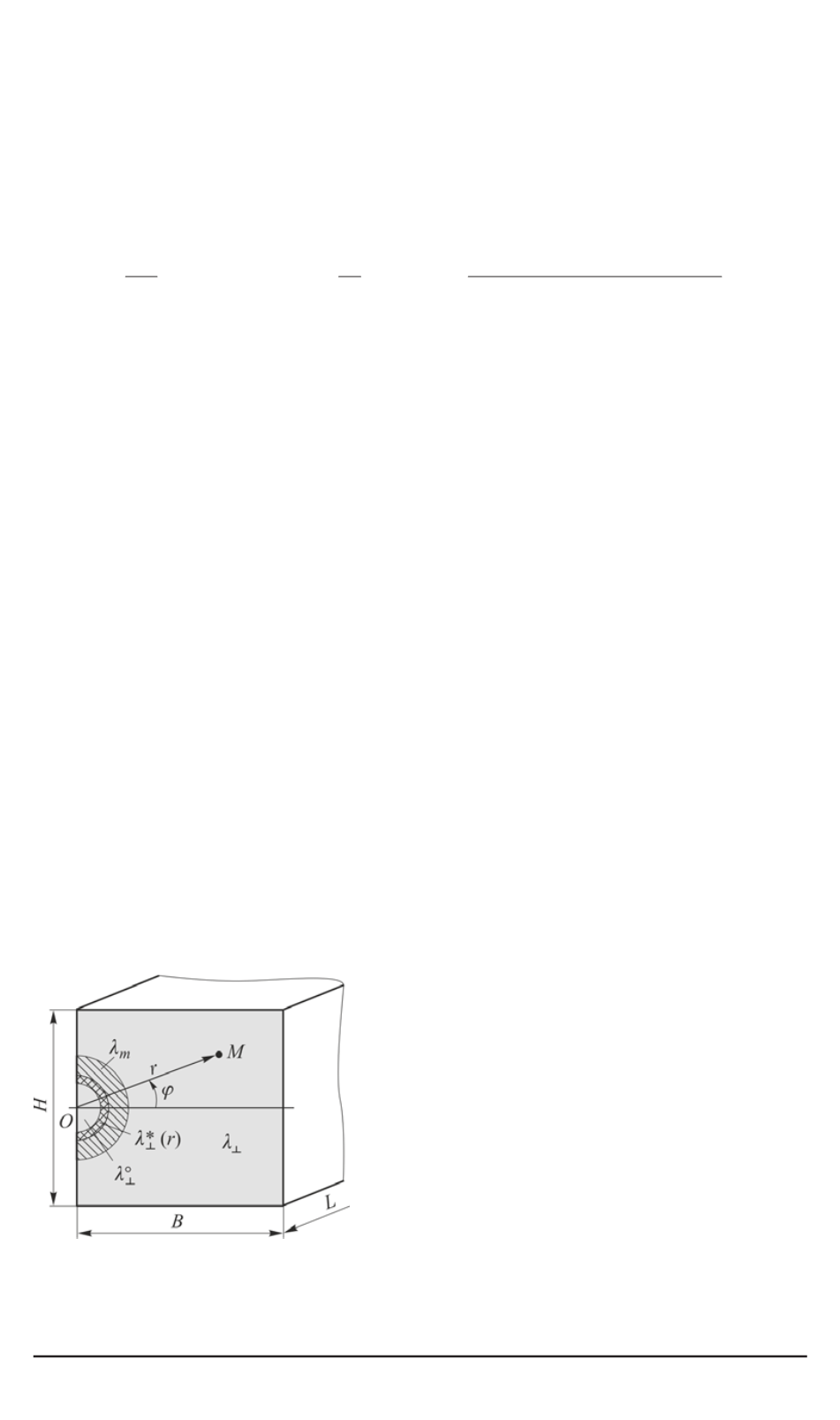
, поперечное сечение которого
плоскостью, перпендикулярной волокну, показано на рис. 1.
Сначала оценим возможную погрешность формулы (11), приняв
температуру боковой грани параллелепипеда, соответствующей в по-
лярных координатах значению
ϕ
=
π/
2
, за нуль отсчета, а темпера-
туру противоположной грани, точки на которой имеют координаты
r
cos
ϕ
=
B
,
B r
m
, положим равной
T
0
=
GH
. Остальные гра-
ни параллелепипеда считаем идеально теплоизолированными. Одно-
родный материал в части области
V
вне составной частицы имеет
Рис. 1. Модель структурыком-
позита для построения двусто-
ронних оценок
коэффициенты теплопроводности
λ
⊥
и
λ
. Таким образом, в неоднородной
области
V
объемом
V
0
=
BHL
, ограни-
ченной поверхностью
S
, распределение
температуры
T
(
M
)
и коэффициент те-
плопроводности
Λ(
M
)
являются функ-
циями координат точки
M
∈
V
, причем
функция
Λ(
M
)
— кусочно-постоянная
и принимает значения
λ
◦
⊥
при
r
≤
r
0
,
λ
∗
(
r
) =
λ
∗
exp(
ar
)
при
r
0
≤
r
≤
r
1
,
λ
m
при
r
1
≤
r
≤
r
m
и
λ
⊥
при
r
≥
r
m
.
8 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2013. № 4


