
жидкости являются фактором, раскачивающим стержень, а не тормозя-
щим его движение. При этом считается, что горизонтальное движение
жидкости обусловлено ее перетеканием с гребня одной волны через
впадину на гребень другой волны (рис. 3,
а
).
При этом интенсивность воздействия на стержень зависит от ско-
рости
˙
h
(
t
)
и ускорения
¨
h
(
t
)
изменения во времени высот волн
h
(
t
)
на поверхности моря. Эти высоты волн считаются гауссовыми ста-
ционарными процессами и задаются спектральной плотностью
S
h
(
ω
)
.
С приближением ко дну эффективная высота волн меняется, например,
как
h
(
x, t
) =
x
l
h
(
t
)
(14)
и интенсивность их воздействия уменьшается. Можно принять, что с
удалением от поверхности моря спектральные плотности скоростей и
ускорений изменяются в соответствии с формулами
S
˙
h
(
ω, x
) =
ω
2
S
h
(
ω
)
x
2
l
2
0
;
(15)
S
¨
h
(
ω, x
) =
ω
4
S
h
(
ω
)
x
2
l
2
0
,
(16)
где
x
— расстояние от дна до рассматриваемого стержня;
l
0
— длина
подводной части сооружения.
Обозначим, как и ранее, через
V
(
x, t
)
— упругое перемещение
стержня в сечении с координатой
x
в момент времени
t
. Дифференци-
альное уравнение колебаний стержня можно принять в виде
μ
∂
2
V
∂t
2
=
CV
=
q
(
x, t
)
,
(17)
где все обозначения прежние, а распределенная нагрузка от воздей-
ствия воды состоит из инерционной и скоростной составляющих и
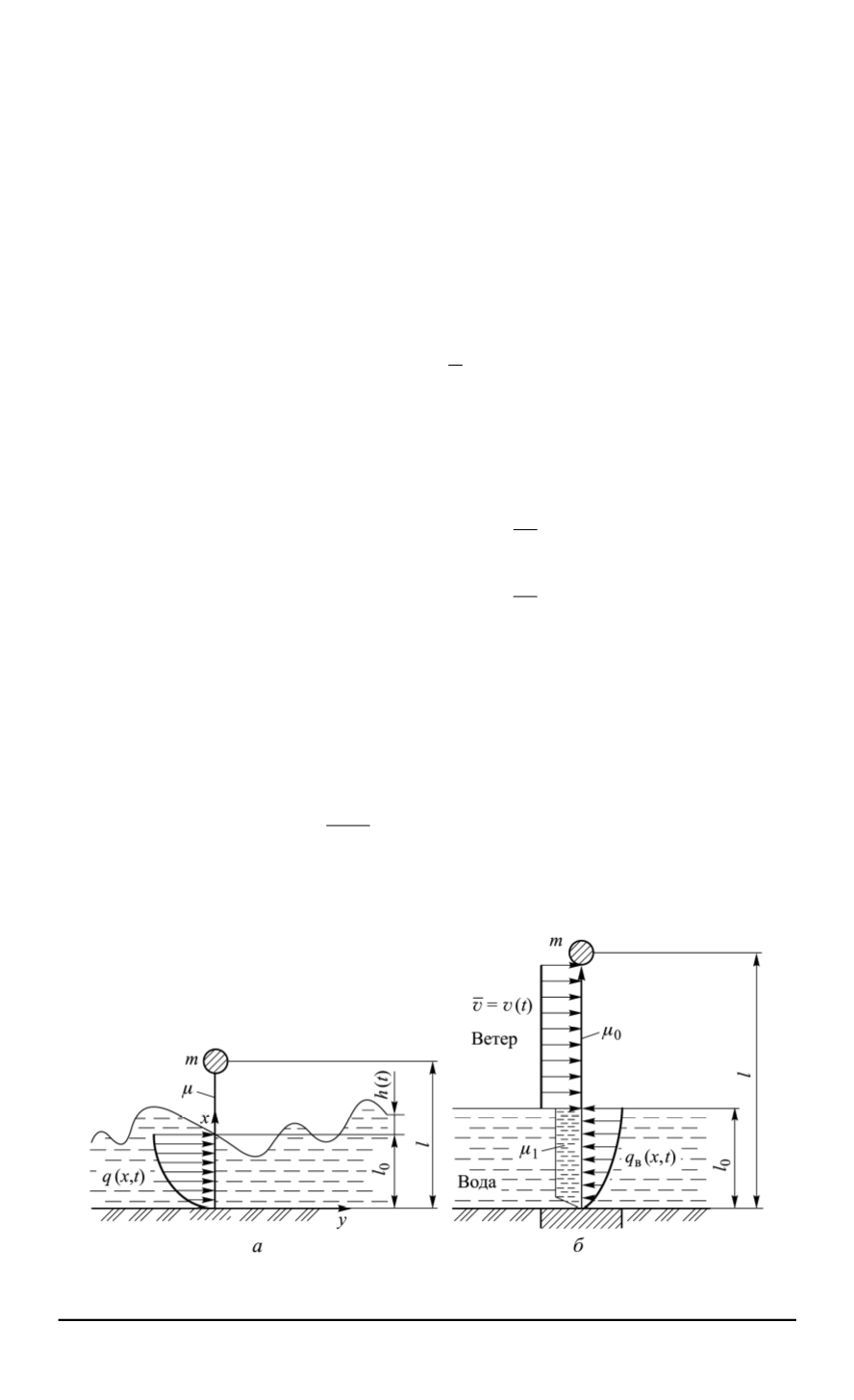
Рис. 3. Расчетная схема при анализе волнового (
а
) и ветрового (
б
) воздействий
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение” 2016. № 2 87
















