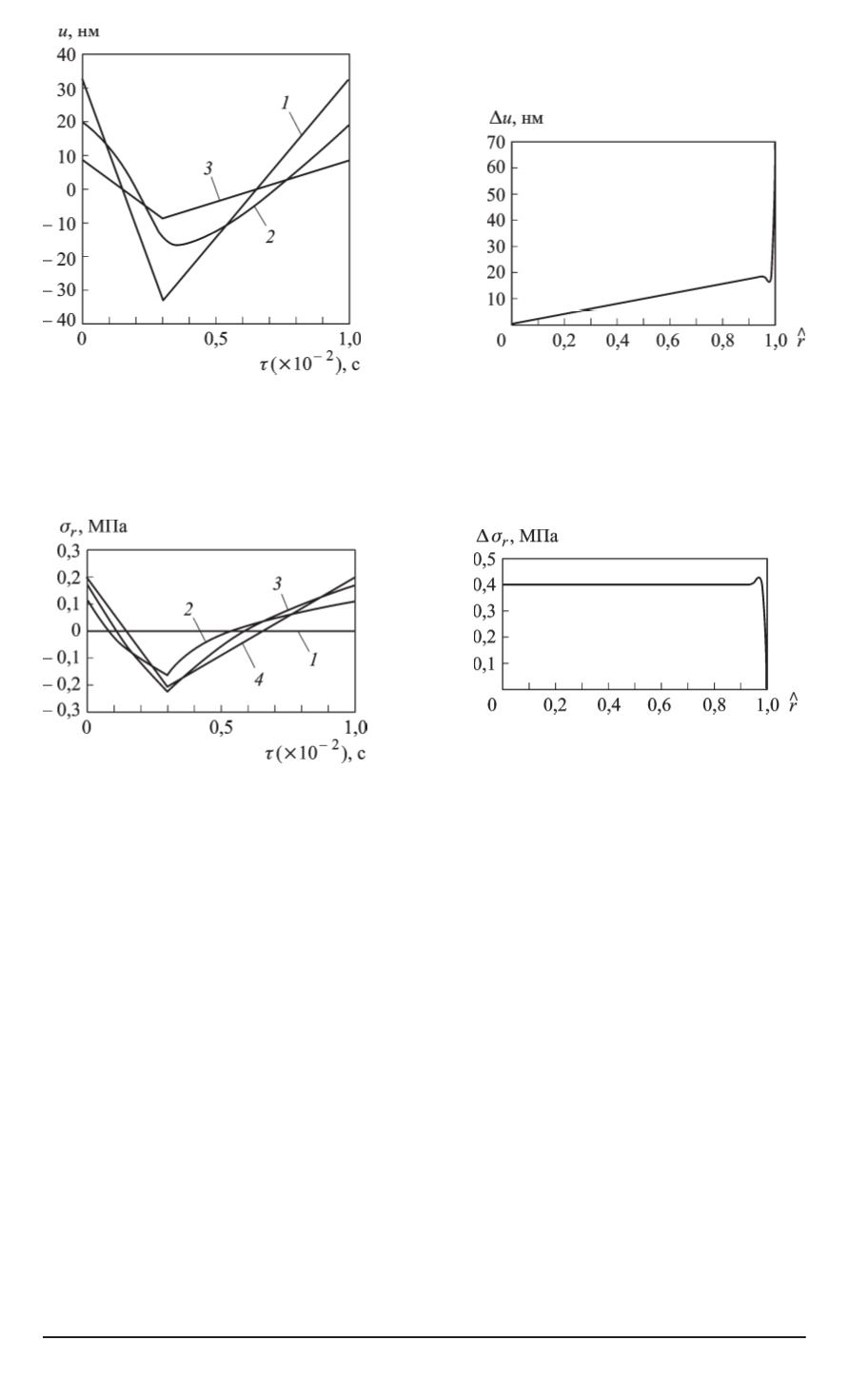
Рис. 3. Зависимость радиальных
перемещений от времени на ра-
диусах:
1
— 0,015 м;
2
— 0,0149 м;
3
—
0,014 м
Рис. 4.
Зависимость размаха
колебаний радиальных переме-
щений от безразмерного радиуса
Рис. 5. Зависимость радиальных
напряжений от времени на ради-
усах:
1
— 0,015 м;
2
— 0,0149 м;
3
—
0,0148 м;
4
— 0,014 м
Рис. 6. Зависимость размаха коле-
баний радиальных напряжений
от безразмерного радиуса
того, зависимости размахов колебанийперемещенийи напряженийот
радиуса не являются монотонными, что наиболее отчетливо видно из
рис. 4 и 6 (на остальных рисунках это незаметно из-за масштаба изо-
бражения). При отсутствии давления среды радиальные напряжения
довольно малы и основное влияние на прочность оказывают окружные
и осевые напряжения, размах колебанийкоторых на поверхности со-
ставляет порядка
60
МПа. В то же время, что наглядно демонстрируют
рис. 7–10, эти напряжения довольно близки между собой.
Результаты расчетов показали, что для рассмотренного случая ква-
зистатическое и динамическое решения дают практически идентич-
ные результаты, тем самым подтверждая гипотезу о малом влиянии
инерционного члена в уравнении (1). Этот факт является важным при
использовании численных методов, поскольку решение гиперболиче-
ского уравнения (1) сопряжено с определенными трудностями. Как
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2012. № 2 55


