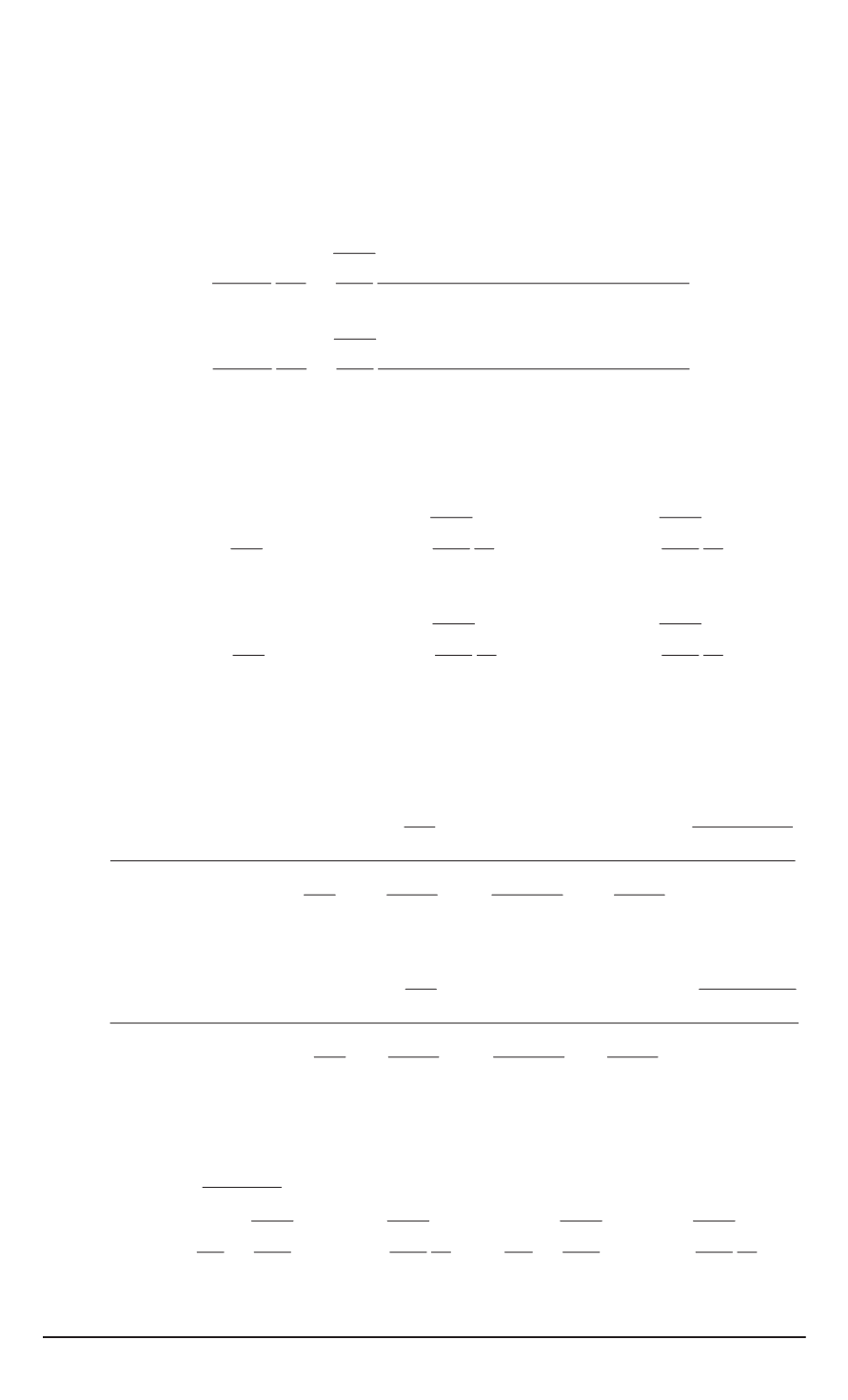
Здесь
J
1
(
x
)
,
Y
1
(
x
)
— функции Бесселя первого порядка 1-го и 2-го
рода соответственно. Значения коэффициентов
φ
u
n
и
χ
u
n
определяют-
ся из решения системы двух алгебраических уравнений, получаемой
подстановкойодного из частных решенийв соответствующее ему диф-
ференциальное уравнение и последующими упрощениями с исполь-
зованием свойств бесселевых функций [9]:
φ
u
n
=
1 +
μ
1
−
μ
α
T
R
n
Fo
∗
(
nω/c
)
2
A
T
n
−
[
n/
(Fo
∗
R
2
)]
B
T
n
(
nω/c
)
4
+
n
2
/
(Fo
∗
R
2
)
2
,
χ
u
n
=
1 +
μ
1
−
μ
α
T
R
n
Fo
∗
(
nω/c
)
2
B
T
n
+ [
n/
(Fo
∗
R
2
)]
A
T
n
(
nω/c
)
4
+
n
2
/
(Fo
∗
R
2
)
2
.
Поскольку из граничных условийзадачи (11) и (12) в центре цилиндра
очевидно, что
C
u
n
=
D
u
n
= 0
, то после суммирования общих и частных
решенийполучаем
˜
A
u
n
(
r
) =
A
u
n
J
1
nω
c
r
+
φ
u
n
ber
n
Fo
∗
r
R
+
χ
u
n
bei
n
Fo
∗
r
R
,
(14)
˜
B
u
n
(
r
) =
B
u
n
J
1
nω
c
r
−
φ
u
n
bei
n
Fo
∗
r
R
+
χ
u
n
ber
n
Fo
∗
r
R
.
(15)
Значения коэффициентов
A
u
n
и
B
u
n
определяются из граничных
условийзадач (11) и (12) на поверхности цилиндра:
A
u
n
=
(1+
μ
)
α
T
˜
A
T
n
(
R
)
−
(1
−
2
μ
)
A
p
n
E
−
(1
−
μ
) ˜
A
u
n
(
R
)
−
μ
˜
A
u
n
(
R
)
R
(1
−
μ
)
nω
c
J
0
nωR
c
−
1
−
2
μ
R
J
1
nωR
c
,
B
u
n
=
(1+
μ
)
α
T
˜
B
T
n
(
R
)
−
(1
−
2
μ
)
B
p
n
E
−
(1
−
μ
) ˜
B
u
n
(
R
)
−
μ
˜
B
u
n
(
R
)
R
(1
−
μ
)
nω
c
J
0
nωR
c
−
1
−
2
μ
R
J
1
nωR
c
,
где
˜
A
u
n
(
r
) =
d
˜
A
u
n
dr
=
=
φ
u
n
R
n
Fo
∗
ber
n
Fo
∗
r
R
+
χ
u
n
R
n
Fo
∗
bei
n
Fo
∗
r
R
,
52 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2012. № 2


