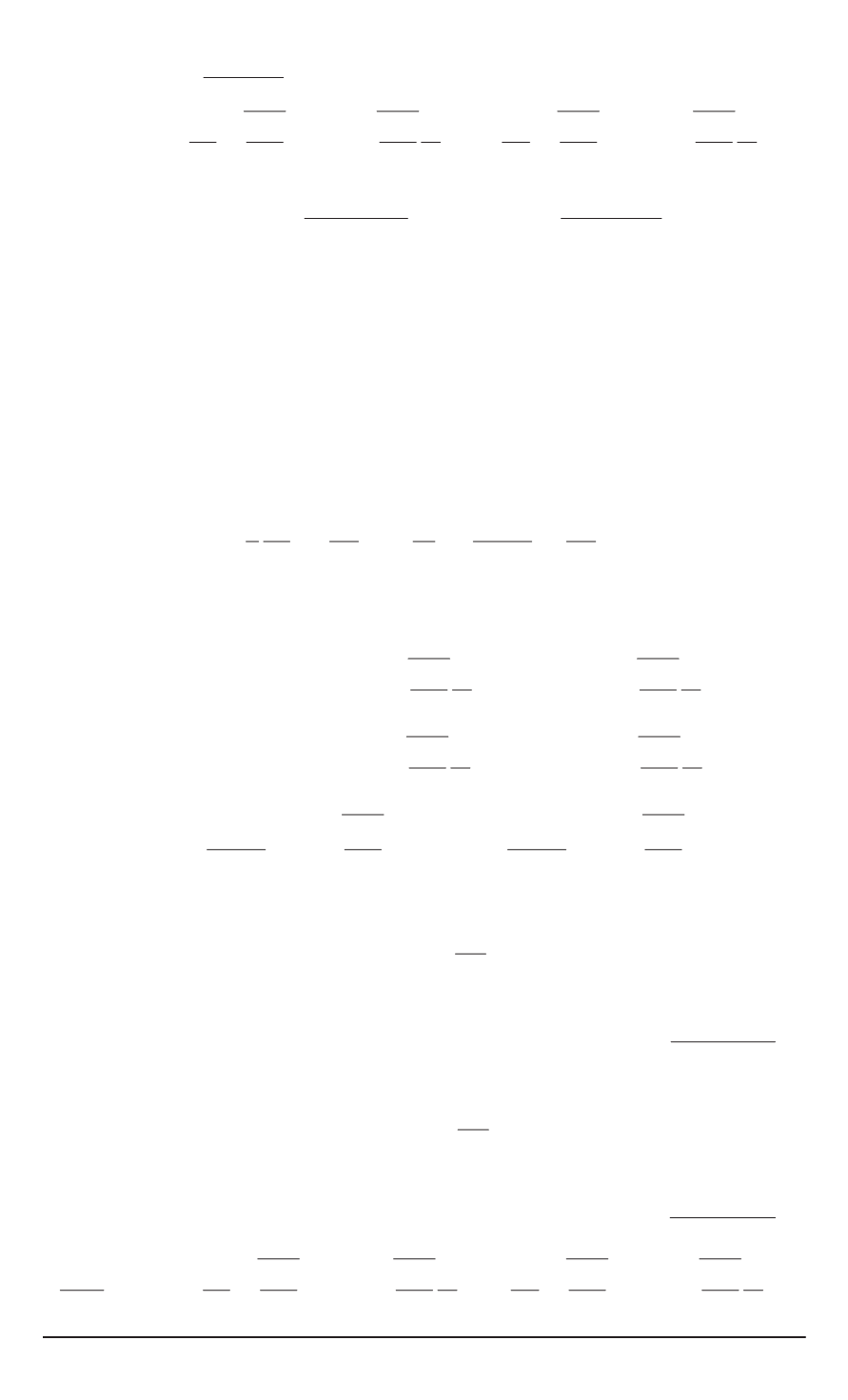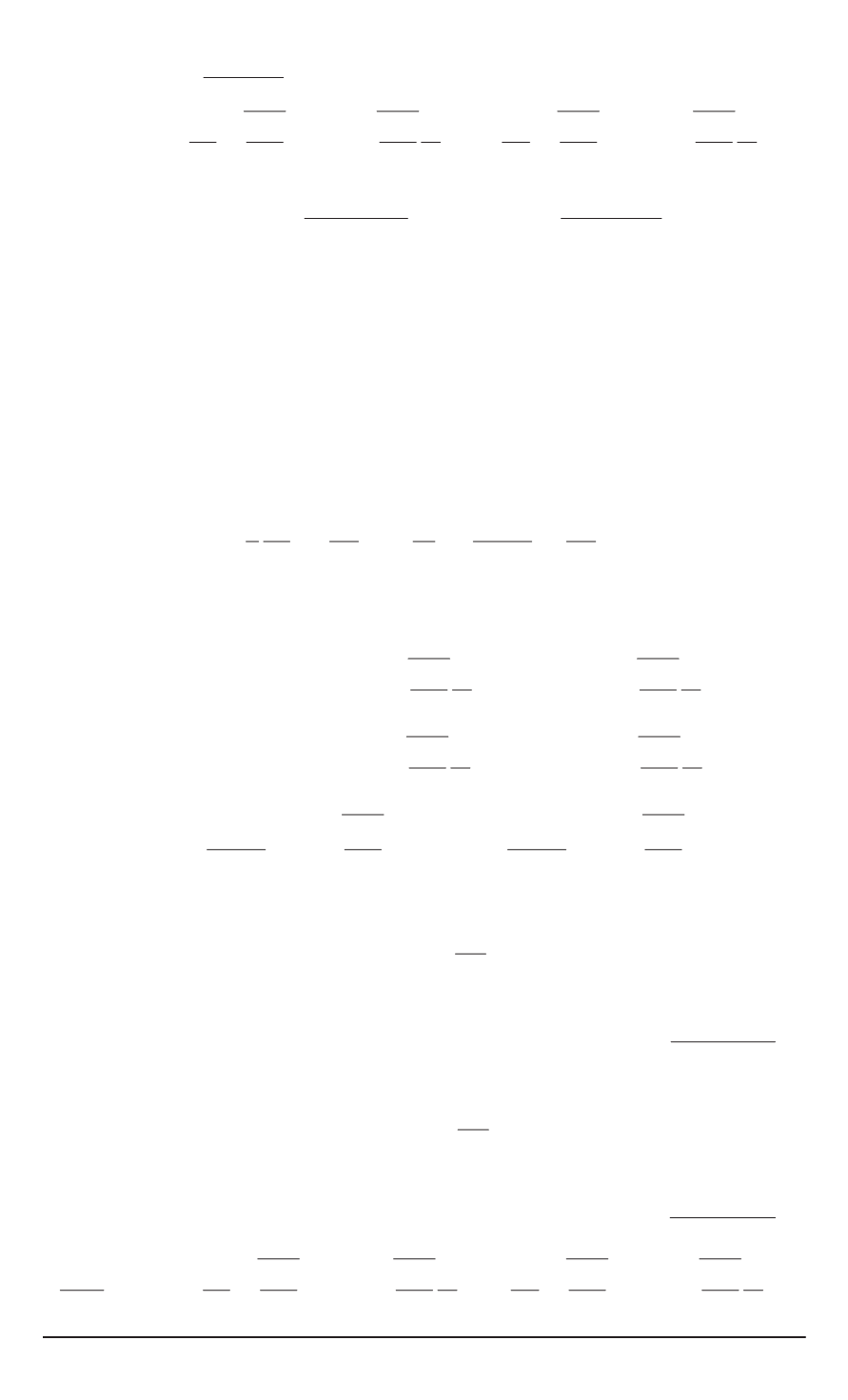
˜
B
u
n
(
r
) =
d
˜
B
u
n
dr
=
=
−
φ
u
n
R
n
Fo
∗
bei
n
Fo
∗
r
R
+
χ
u
n
R
n
Fo
∗
ber
n
Fo
∗
r
R
,
ber (
x
) =
d
2
ber (
x
)
dx
2
,
bei (
x
) =
d
2
bei (
x
)
dx
2
.
Теперь легко найти напряжения с помощью формул (4).
Поскольку уравнение (1) содержит инерционныйчлен, то полу-
ченное решение учитывает динамические эффекты. Однако из-за того,
что в металлах скорость распространения продольных волн достаточ-
но велика и изменения температуры обычно происходят медленно, на
практике часто пренебрегают инерционным членом и ищут решение
задачи в квазистатическойпостановке [6]. В этом случае перемещения
будут описываться уравнением, получаемым из (1) при
c
→ ∞
,
1
r
∂
∂r
r
∂u
∂r
−
u
r
2
=
1 +
μ
1
−
μ
α
T
∂ϑ
∂r
.
Не повторяя рассуждений, отметим лишь те отличия, которые по-
явятся в найденных выражениях:
˜
A
u
n
(
r
) = ˆ
A
u
n
r
+
φ
u
n
ber
n
Fo
∗
r
R
+
χ
u
n
bei
n
Fo
∗
r
R
,
˜
B
u
n
(
r
) = ˆ
B
u
n
r
−
φ
u
n
bei
n
Fo
∗
r
R
+
χ
u
n
ber
n
Fo
∗
r
R
,
φ
u
n
=
−
1 +
μ
1
−
μ
α
T
R
Fo
∗
n
B
T
n
, χ
u
n
=
1 +
μ
1
−
μ
α
T
R
Fo
∗
n
A
T
n
,
ˆ
A
u
n
= (1 +
μ
)
α
T
˜
A
T
n
(
R
)
−
(1
−
2
μ
)
A
p
n
E
−
−
(1
−
μ
) ˜
A
u
n
(
R
)
−
μ
˜
A
u
n
(
R
)
R
,
ˆ
B
u
n
= (1 +
μ
)
α
T
˜
B
T
n
(
R
)
−
(1
−
2
μ
)
B
p
n
E
−
−
(1
−
μ
) ˜
B
u
n
(
R
)
−
μ
˜
B
u
n
(
R
)
R
,
d
˜
A
u
n
dr
= ˆ
A
u
n
+
φ
u
n
R
n
Fo
∗
ber
n
Fo
∗
r
R
+
χ
u
n
R
n
Fo
∗
bei
n
Fo
∗
r
R
,
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2012. № 2 53