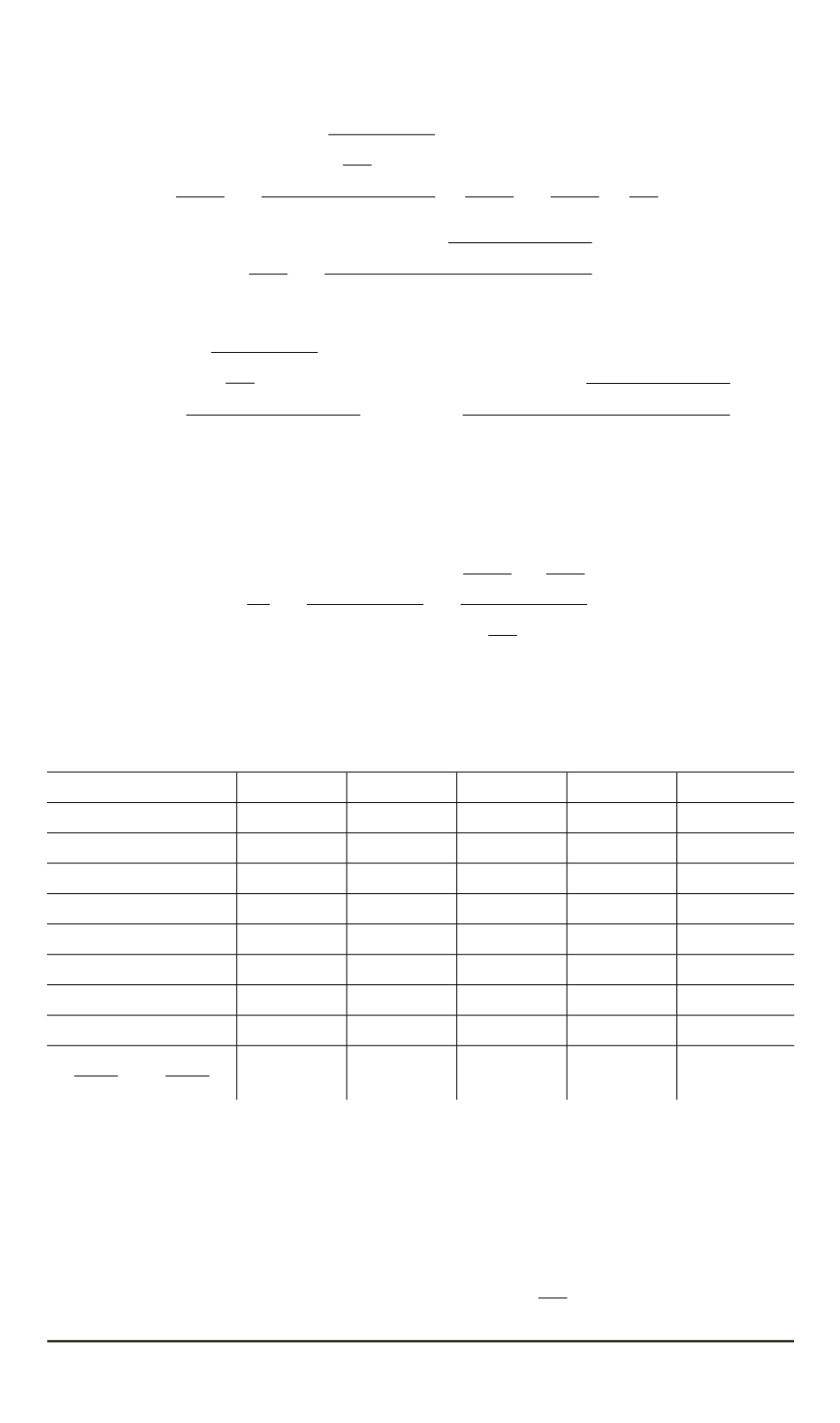
полученные значения сведем в табл. 4. Там же приведены результаты
расчетов радиусов
R
нар
R
2
=
1 +
r
4
R
1
R
2
Z
−
3
2
Z
;
R
нар
R
1
=
R
нар
R
1
R
2
R
2
;
R
вн
R
2
=
2
Z
−
1 +
√
5
−
8
Z
+ 4
Z
2
2
и относительных деформаций
ε
θ
нар
=
r
4
R
1
R
2
Z
−
3
−
1
2
;
ε
θ
вн
=
2
Z
−
3 +
√
5
−
8
Z
+ 4
Z
2
2
.
Полученные значения радиусов изогнутой полосы
R
нар
и
R
вн
будут
определять общую толщину полосы
S
0
после гибки и ее отношение к
начальной толщине (
S
=
R
1
−
R
2
):
S
0
S
=
R
нар
−
R
вн
R
1
−
R
2
=
R
нар
R
2
−
R
вн
R
2
R
1
R
2
−
1
.
Таблица 4
Геометрические и кинематические параметры изогнутой полосы
при соотношении изменяющихся радиусов
R
1
/R
2
1,1
1,3
1,5
2,0
3,0
Z
=
R
2
/ρ
н
0,952
0,868
0,795
0,649
0,465
Z
1
=
ρ
н
/R
1
0,955
0,887
0,839
0,771
0,717
R
нар
/R
2
1,098
1,285
1,466
1,911
2,802
R
нар
/R
1
0,998
0,988
0,977
0,956
0,934
R
вн
/R
2
1,002
1,016
1,036
1,105
1,268
ε
θ
нар
0,045
0,115
0,165
0,24
0,301
ε
r
нар
– 0,043 – 0,103 – 0,140 – 0,194 – 0,232
S
0
/S
0,957
0,897
0,859
0,806
0,768
R
нар
ρ
н
=
Z
R
нар
R
2
1,045
1,115
1,165
1,240
1,303
Анализируя уточненное положение нейтральной поверхности,
определяемой параметрами
Z
и
Z
1
без учета утонения полосы (см.
табл. 2) и с учетом ее утонения (табл. 4), выявили, что процесс утоне-
ния смещает нейтральную поверхность в сторону наружного радиуса,
т.е. в сторону растянутых волокон. Смещение нейтральной поверхно-
сти увеличивается с увеличением отношения
R
1
R
2
. Так, для отношения
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение” 2014. № 5 93


