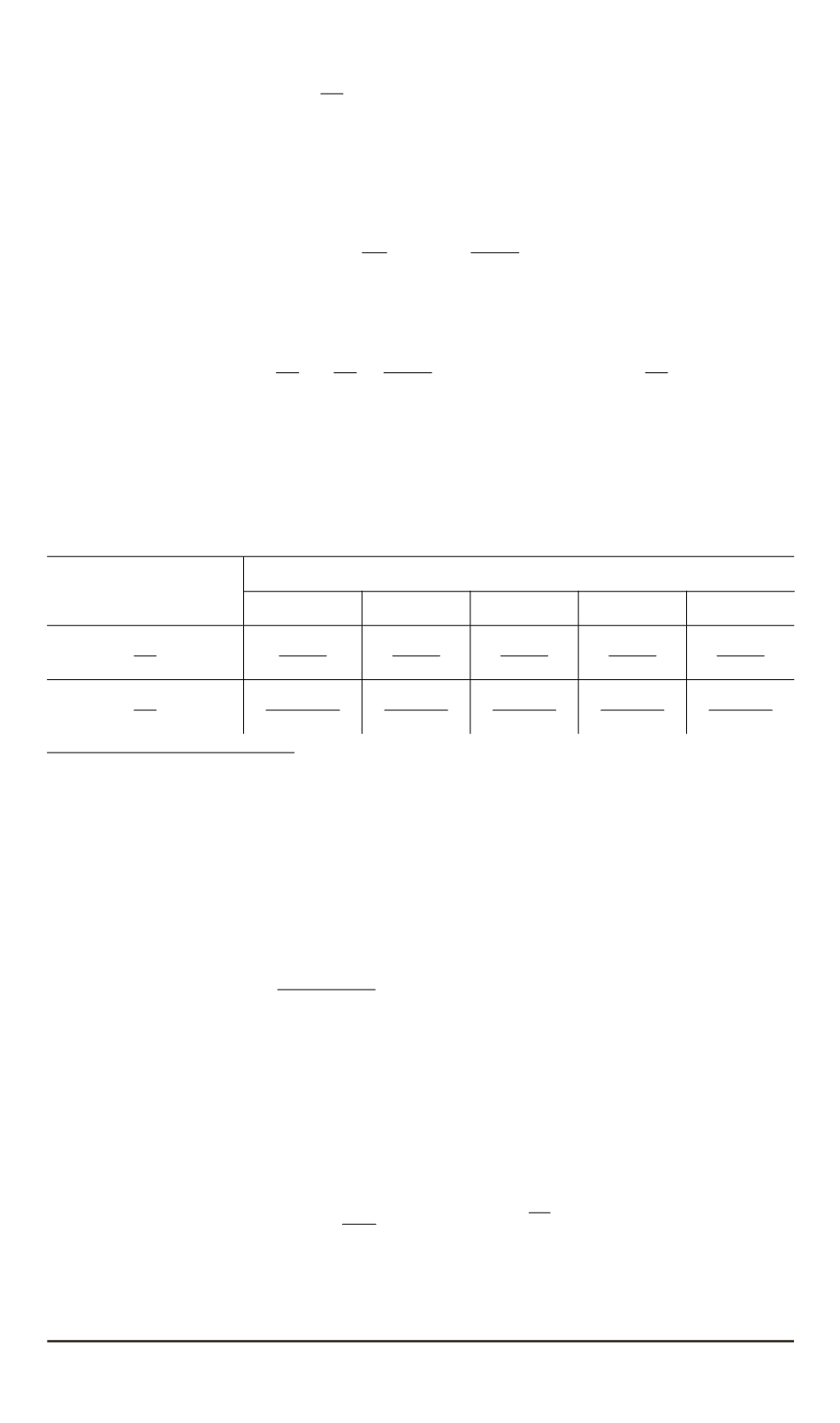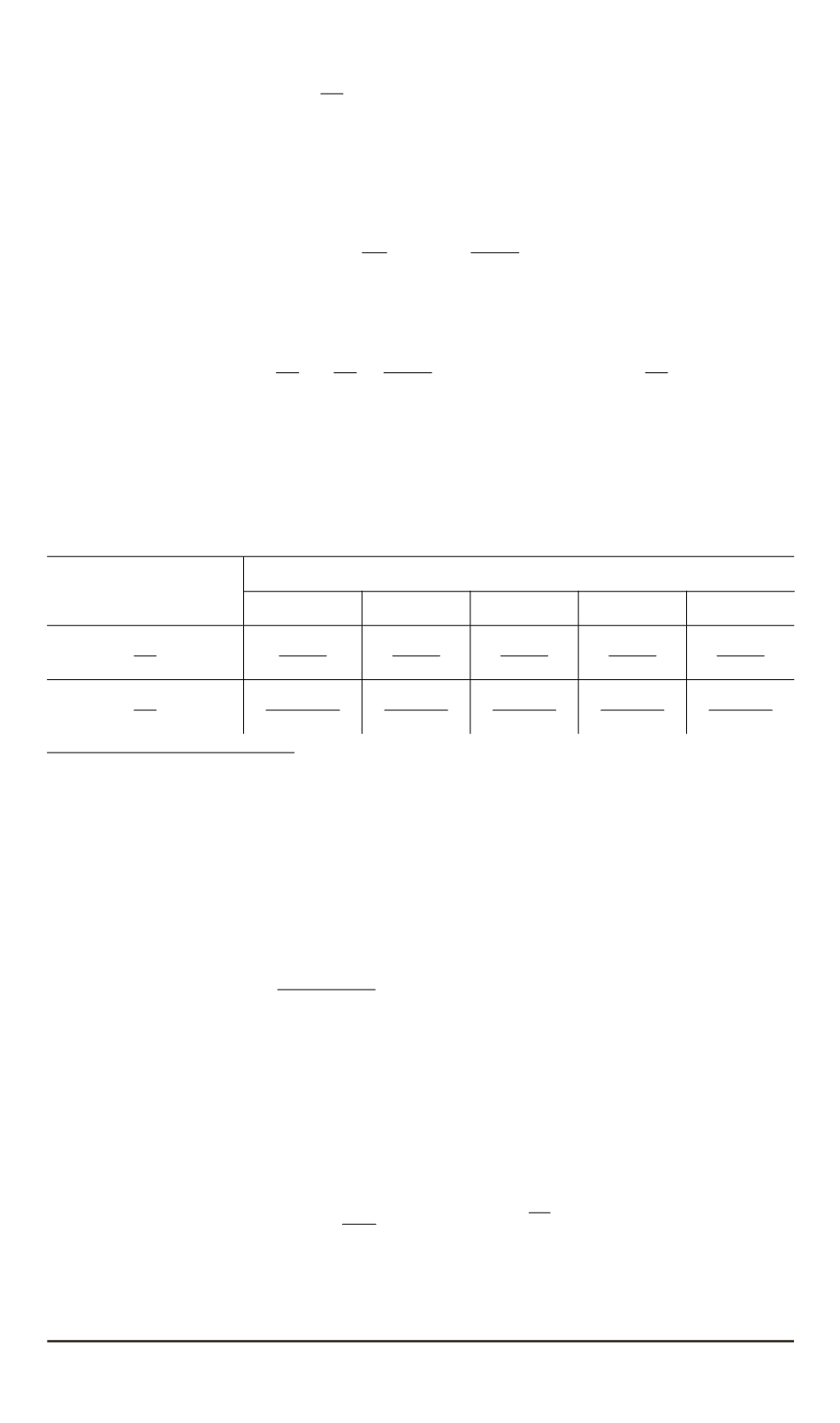
где
k
у
.
т
= (1 + 0
,
666
f
)
S
0
S
2
— коэффициент, учитывающий утоне-
ние.
Максимальное радиальное напряжение без учета упрочнения ста-
новится равным
σ
r
max
=
σ
т
k
1
"
1
−
R
нар
ρ
н
k
1
#
(16)
и тангенциальное напряжение
σ
θ
max
=
σ
т
"
1 +
1
k
1
−
1
k
1
R
нар
ρ
н
k
1
#
(1 + 0
,
666
f
)
S
0
S
2
.
(17)
В табл. 5 приведены результаты расчета указанных напряжений без
учета упрочнения материала.
Таблица 5
Силовые параметры при гибке без учета упрочнения
Параметры гибки
R
1
/R
2
1,1
1,3
1,5
2
3
σ
θ
σ
т
0
,
933
1
,
017
0
,
736
0
,
798
0
,
617
0
,
667
0
,
454
0
,
487
0
,
328
0
,
352
σ
r
σ
т
−
0
,
047
−
0
,
0496
−
0
,
114
−
0
,
123
−
0
,
159
−
0
,
170
−
0
,
223
−
0
,
237
−
0
,
274
−
0
,
288
П р и м е ч а н и е. B числителе напряжения при
f
= 0
,
1
, в знаменателе — при
f
= 0
,
25
В реальных условиях материал полосы в процессе прокатки упроч-
няется [11]. Наиболее точно процесс упрочнения описывается степен-
ной зависимостью
σ
т
=
σ
т
0
+
Kε
00
,
(18)
где
σ
т
0
— начальное значение сопротивления пластической деформа-
ции при
ε
= 0
;
K
=
σ
тк
−
σ
т
0
ε
00
к
— параметр упрочнения;
σ
тк
— конеч-
ное значение сопротивления пластической деформации, отвечающее
деформации
ε
=
ε
к
; обычно
ε
к
= 0
,
5
, что определяет
σ
тк
≈
(2
. . .
3)
σ
т
0
(для углеродистых сталей, сплавов алюминия и меди);
n
— показатель
упрочнения, зависит от вида материала и изменяется от 0,32 до 0,85
(в среднем
n
≈
0
,
5
).
Для предварительных расчетов коэффициента упрочнения имеем
k
у
=
σ
т
σ
т
0
= 1 + 1
,
414
√
ε
θ
.
(19)
Далее в табл. 6 приведены значения коэффициента упрочнения и
соответствующие напряжения
σ
θ
и
σ
r
.
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение” 2014. № 5 95