Решение относительно
Z
1
определяет ее значение:
Z
1
= 0
,
954
или
Z
=
1
Z
1
R
1
R
2
=
1
0
,
954
∙
1
,
1
= 0
,
953
.
Соответственно
ρ
н
= 0
,
9535
R
1
. Представим радиус нейтральной
поверхности через
ρ
н
=
Z
1
R
1
R
2
R
2
= 1
,
049
R
2
. Откуда для отношения
R
1
R
2
= 1
,
1
нейтральный радиус
ρ
н
=
√
R
1
R
2
.
Таким образом, для первого приближенного расчета, пренебрегая
изменением толщины полосы в месте гиба, положение нейтральной
поверхности рассчитывается по формуле Е.А. Попова.
При увеличении коэффициента трения до
f
= 0
,
25
параметры
k
1
= 5
,
369
и
k
2
= 4
,
87
. Тогда уравнение связи (5) принимает вид
0
,
326
Z
4
,
87
1
−
0
,
186
Z
5
,
369
1
= 0
,
0193
.
Его решением будет
Z
1
= 0
,
954
и
Z
=
1
0
,
954
∙
1
,
1
= 0
,
953
, что также
определяет
ρ
н
=
√
R
1
R
2
.
В табл. 2 приведены значения нейтрального радиуса по равенству
радиальных напряжений на границе зон растяжения и сжатия для раз-
личных отношений
R
1
R
2
и разных коэффициентов трения
f
= 0
,
1
и
f
= 0
,
25
для первых проходов.
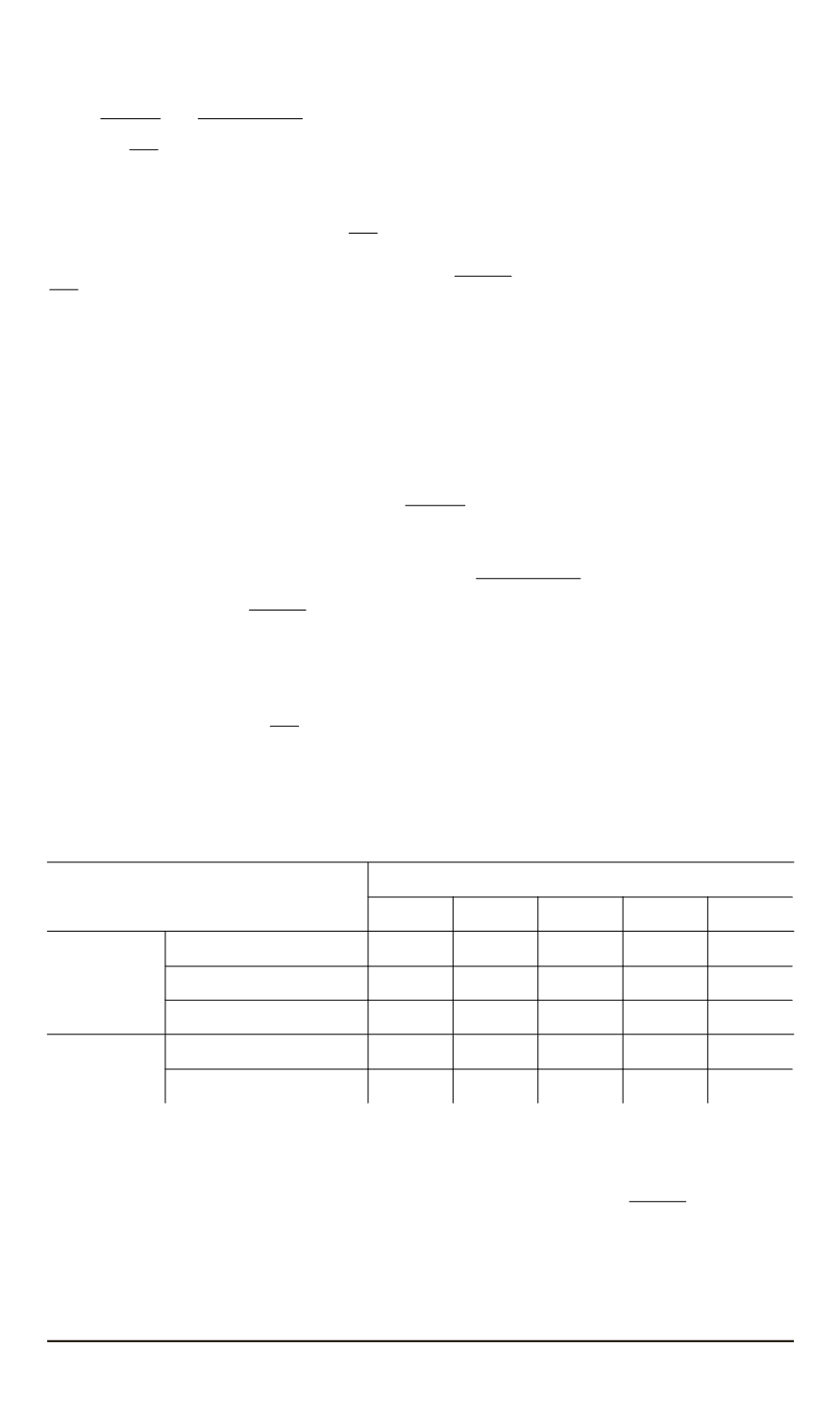
Таблица 2
Значения нейтрального радиуса
Параметры гибки
R
1
/R
2
1,1
1,3
1,5
2
3
f
= 0
,
1
Z
1
=
ρ
н
/
R
1
0,954 0,878 0,818 0,710 0,590
Z
1
=
ρ
н
/
R
1
по [7]
0,953 0,877 0,816 0,707 0,580
Z
=
R
2
/ρ
н
0,953 0,876 0,815 0,704 0,565
f
= 0
,
25
Z
1
=
ρ
н
/R
1
0,954 0,879 0,820 0,717 0,600
Z
=
R
2
/ρ
н
0,953 0,875 0,813 0,697 0,555
Анализируя табличные данные выявили, что в качестве первого
приближения с ошибкой до 2% для определения радиуса нейтральной
поверхности можно использовать зависимость
ρ
н
=
√
R
1
R
2
.
По выражению (5) и формуле Е.А. Попова (7) рассчитаны мак-
симальные радиальные напряжения (табл. 3), действующие на ней-
тральной поверхности. Там же приведено сравнение напряжений
90 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2014. № 5


