Δ
1
=
σ
r
max 1
−
σ
r
max 2
σ
r
max 2
∙
100 %
для минимального коэффициента тре-
ния
f
= 0
,
1
и аналогичное отношение
Δ
2
для коэффициента трения
f
= 0
,
25
.
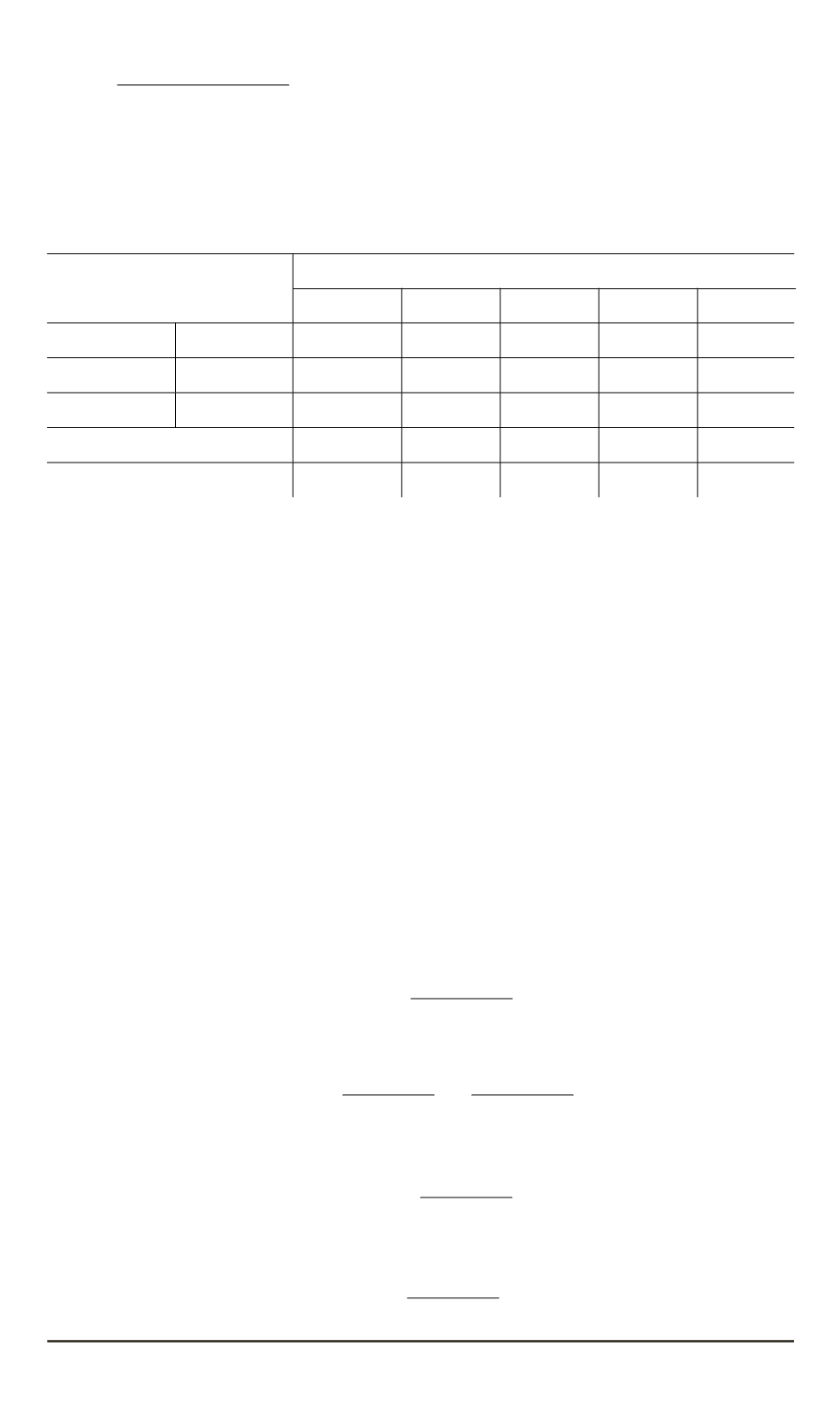
Таблица 3
Максимальные напряжения
σ
r
max 1
и
σ
r
max 2
Параметры гибки
R
1
/R
2
1,1
1,3
1,5
2
3
f
= 0
,
1
σ
r
max 1
0,0507
0,138
0,215
0,357
0,565
f
= 0
,
25
σ
r
max 1
0,0549
0,151
0,234
0,374
0,589
f
= 0
σ
r
max 2
0,0476
0,131
0,202
0,346
0,549
Δ
1
, %
6,5
5,3
6,4
3,2
3,5
Δ
2
, %
15,3
15,3
15,8
8,1
7,3
Из табл. 3 следует, что на первых проходах, когда утонение изгиба-
емой полосы ничтожно, значения радиуса нейтральной поверхности
и радиальные напряжения, определенные по двум методикам, имеют
небольшое расхождение. Однако анализ приведенных данных показы-
вает, что с увеличением трения значительно возрастают радиальные
напряжения.
На следующих проходах геометрические и кинематические пара-
метры гибки изменяют размеры радиусов
R
1
и
R
2
на соответствую-
щие, деформированные: наружный
R
нар
и внутренний
R
вн
:
R
нар
=
R
1
+ (
R
1
−
ρ
н
)
ε
r
нар
,
R
вн
=
R
2
+ (
ρ
н
−
R
2
)
ε
r
вн
.
(8)
Относительную радиальную деформацию
ε
r
определим через тан-
генциальную деформацию. Тогда для зоны растяжения
ε
θ
нар
=
R
нар
−
ρ
н
ρ
н
и соответственно
ε
r
нар
=
−
ε
θ
нар
1 +
ε
θ
нар
=
ρ
н
−
R
нар
R
нар
.
Для зоны сжатия
ε
θ
вн
=
−
ρ
н
−
R
вн
ρ
н
и соответственно
ε
r
вн
=
ρ
н
−
R
вн
R
вн
.
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение” 2014. № 5 91


