Действующее в материале стержня среднее давление
σ
(дающее в
сумме со значением
s
z
осевое напряжение
σ
z
) определялось с привле-
чением уравнения движения частиц стержня в радиальном направле-
нии, записываемого в пренебрежении влиянием касательных напря-
жений
τ
zr
в виде
ρ
dv
r
dt
=
∂s
r
∂r
+
∂σ
∂r
.
Проинтегрировав данное уравнение по радиусу стержня от неко-
торого его текущего значения
r
до радиуса наружной поверхности
R
,
получим радиальное распределение среднего напряжения
σ
(
r
) =
s
r
(
R
)
−
s
r
(
r
) +
σ
(
R
)
−
ρ
R
Z
r
dv
r
dt
dr,
(6)
в котором среднее напряжение на боковой поверхности стержня
σ
(
R
)
можно определить из динамического граничного условия (записыва-
емого, по-прежнему, в пренебрежении влиянием касательных напря-
жений
τ
zr
) равенства полного напряжения на поверхности стержня
магнитному давлению
p
m
, взятому с противоположным знаком:
(
s
r
(
R
) +
σ
(
R
)) cos
2
α
+ (
s
z
(
R
) +
σ
(
R
)) sin
2
α
=
−
p
m
,
где
α
— угол наклона касательной к боковой поверхности стержня в
данном сечении (рис. 3).
Приняв во внимание приведенное граничное условие, а также то,
что в соответствии с (4)
dv
r
dt
=
∂v
r
∂t
+
v
r
∂v
r
∂r
=
r
4
˙
ε
2
z
−
2
d
˙
ε
z
dt
,
можно переписать (6) в виде
σ
(
r
) =
−
s
r
(
r
)
−
(
s
z
(
R
)
−
s
r
(
R
)) sin
2
α
−
ρ
8
˙
ε
2
z
−
2
d
˙
ε
z
dt
R
2
−
r
2
−
p
m
.
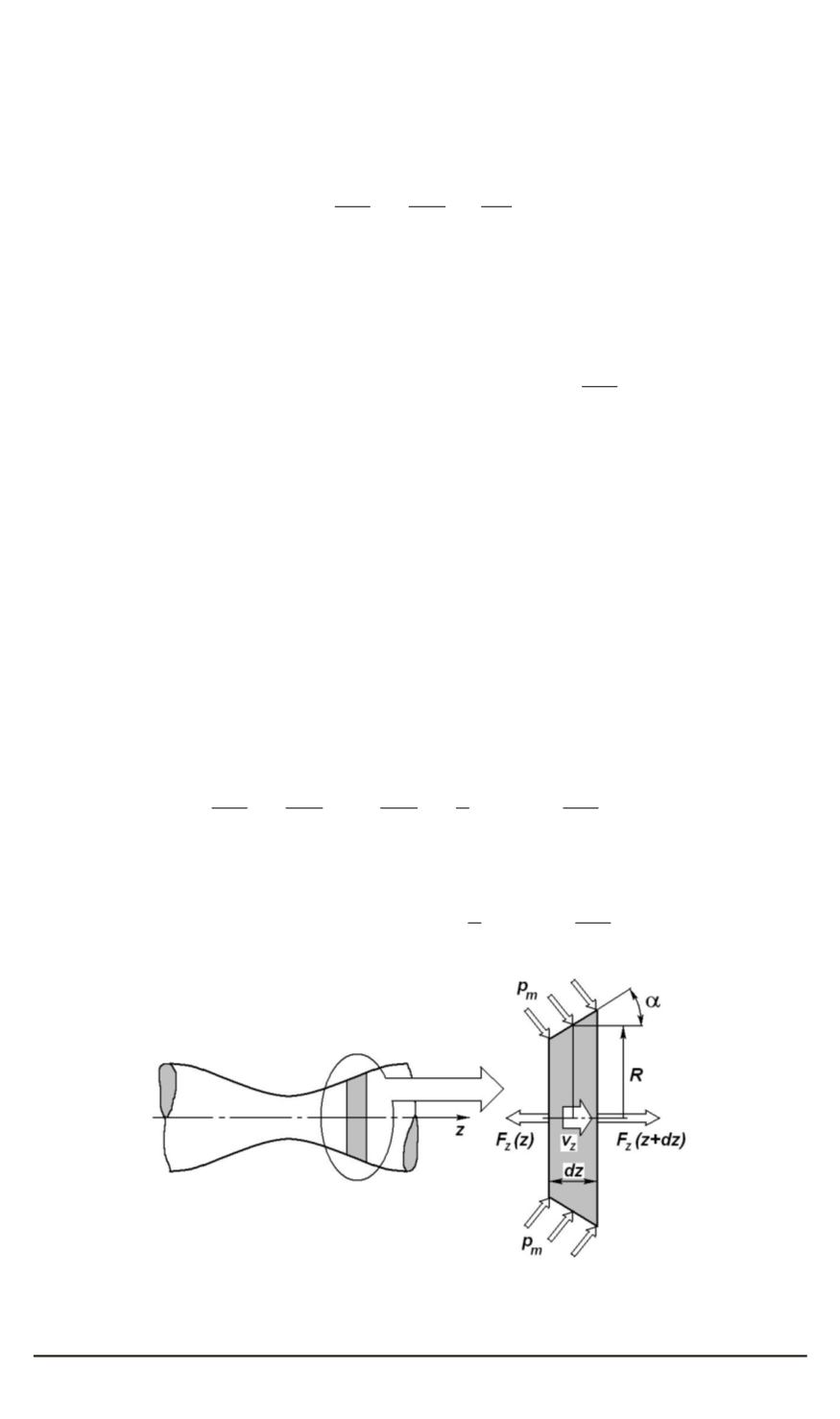
Рис. 3. Расчетная схема деформирования участка кумулятивной струи при
пропускании по нему электрического тока
84 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2014. № 3


