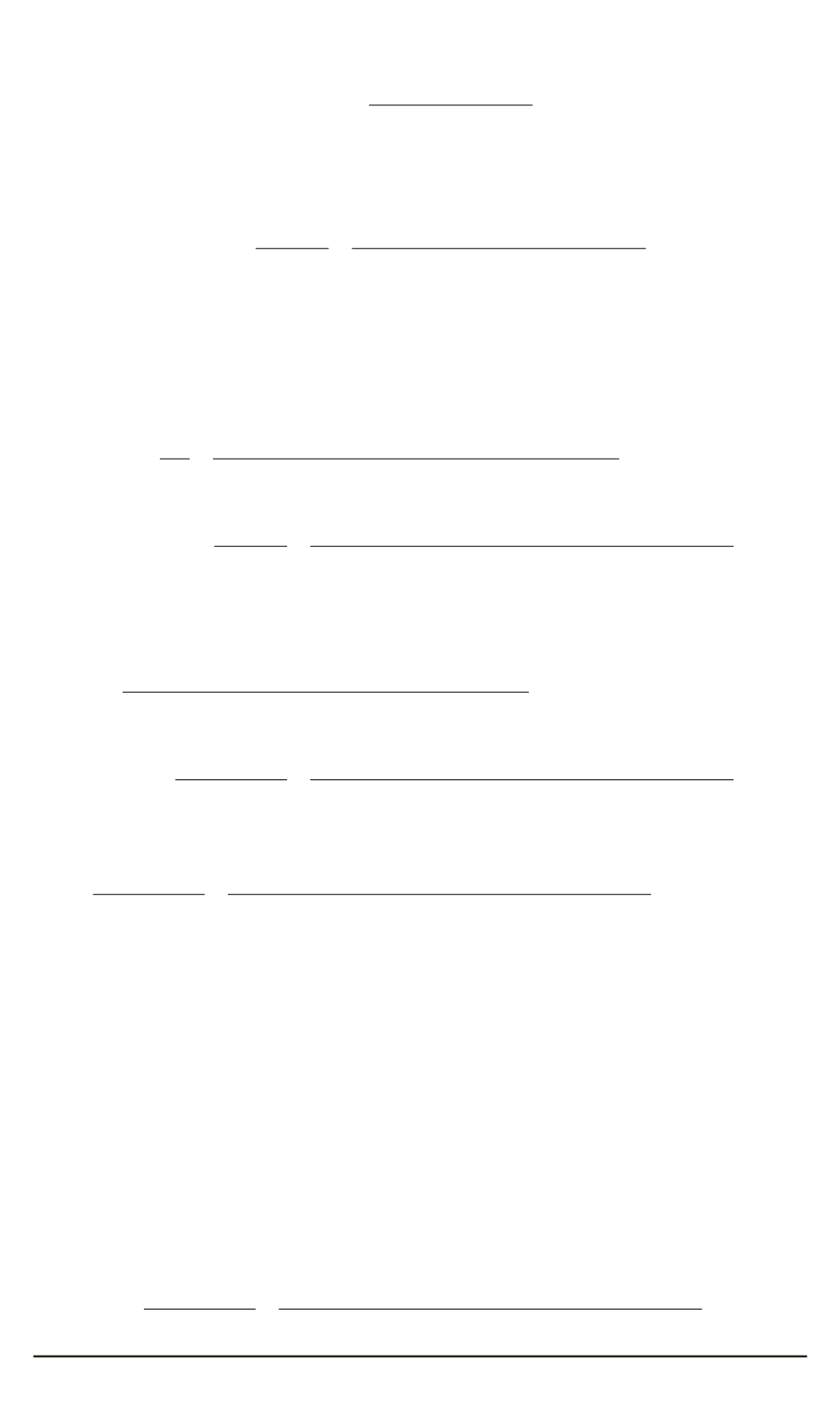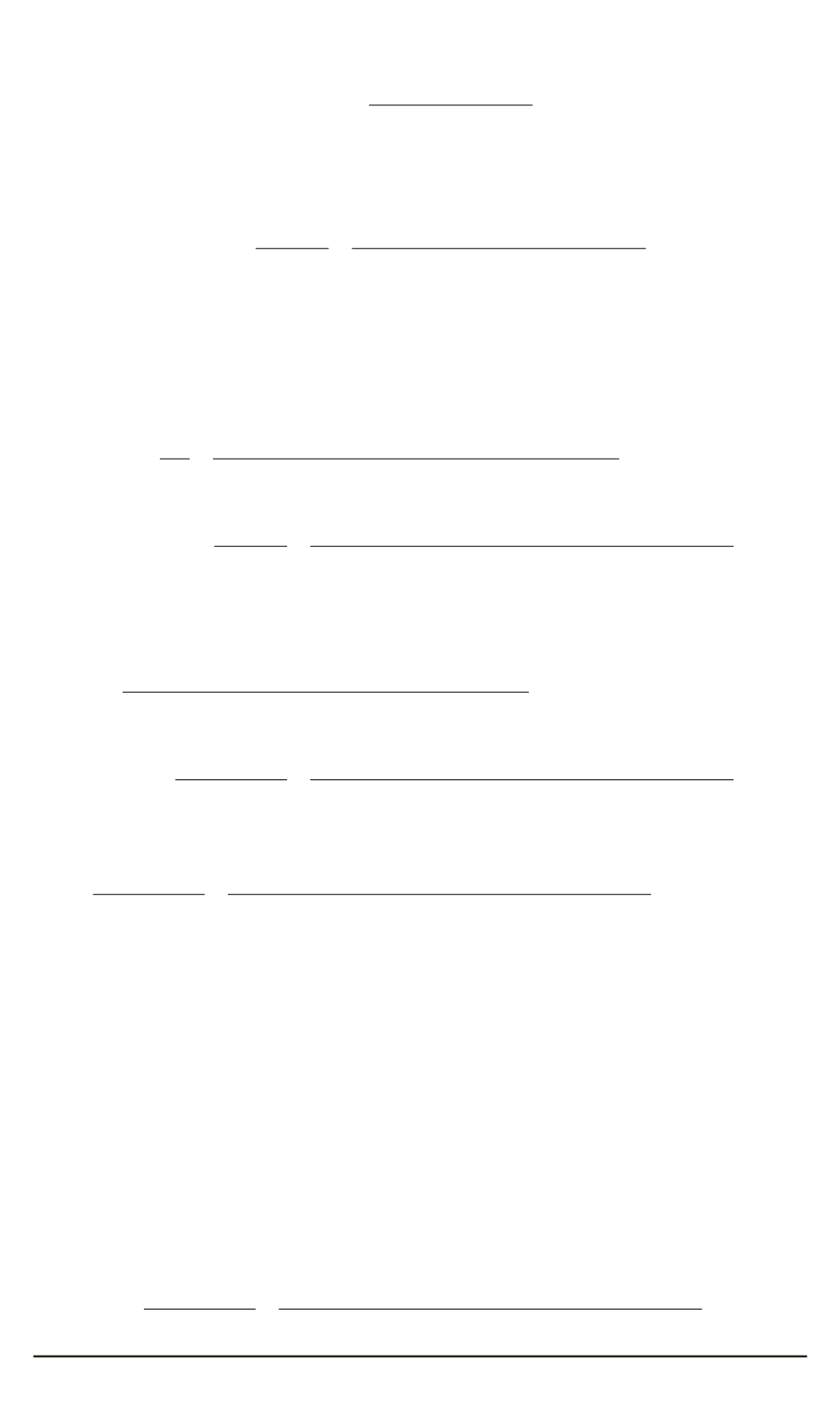
Условие двустороннего контакта зубьев следующее:
M
2
<
F
2
r
b
2
(1
−
k
0
21
)
(1 +
k
0
0
) sin
α
tw
.
(33)
Заменяя введенные коэффициенты их исходными выражениями
(12) и (13), получаем:
M
2
<
F
2
r
b
2
sin
α
tw
∙
cos
β
b
tan
α
tw
−
f
12
tan
α
ty
2
cos
β
b
tan
α
tw
+
f
12
.
(34)
В отличие от прямого хода, при моменте
M
2
большем, чем правая
часть условия (34), здесь появляется зазор в зацеплении.
Момент
M
1
может быть определен после подстановки значений
проекций нормальных усилий из (31) и (32) в уравнение (30):
M
1
=
M
2
r
b
1
r
b
2
∙
(1 +
k
0
0
) (1 +
k
00
12
) + (1
−
k
00
0
) (1
−
k
0
12
)
(1
−
k
00
0
) (1
−
k
0
21
) + (1 +
k
0
0
) (1 +
k
00
21
)
−
−
F
2
r
b
1
sin
α
tw
∙
(1 +
k
00
12
) (1
−
k
0
21
)
−
(1
−
k
0
12
) (1 +
k
00
21
)
(1
−
k
00
0
) (1
−
k
0
21
) + (1 +
k
0
0
) (1 +
k
00
21
)
.
(35)
В соответствии с (24) и (35) КПД обратного хода
η
21
определится
так:
η
21
=
(1 +
k
0
0
) (1 +
k
00
12
) + (1
−
k
00
0
) (1
−
k
0
12
)
(1
−
k
00
0
) (1
−
k
0
21
) + (1 +
k
0
0
) (1 +
k
00
21
)
−
−
F
2
r
b
2
M
2
sin
α
tw
∙
(1 +
k
00
12
) (1
−
k
0
21
)
−
(1
−
k
0
12
) (1 +
k
00
21
)
(1
−
k
00
0
) (1
−
k
0
21
) + (1 +
k
0
0
) (1 +
k
00
21
)
.
(36)
Из уравнения (36) следует условие самоторможения:
F
2
r
b
2
M
2
sin
α
tw
∙
(1 +
k
00
12
) (1
−
k
0
21
)
−
(1
−
k
0
12
) (1 +
k
00
21
)
(1
−
k
00
0
) (1
−
k
0
21
) + (1 +
k
0
0
) (1 +
k
00
21
)
>
1
.
(37)
Таким образом, зубчатые передачи с гибким венцом одного из ко-
лес могут быть выполнены как самотормозящимися, так и без само-
торможения. При этом отсутствие зазора в зацеплении может быть как
на всем заданном диапазоне нагрузок, так и на отдельном его участке.
Если несамотормозящаяся передача работает только в тяговом режи-
ме, то отсутствие зазора в зацеплении может быть обеспечено без
предварительного натяга. Для этого достаточно обеспечить возмож-
ность радиального перемещения участка зацепления одного из венцов
или самого венца.
Коэффициент оттормаживания
μ
12
самотормозящейся передачи в
соответствии со схемой на рис. 2,
в
также следует из уравнения (36):
μ
21
=
F
2
r
b
2
M
2
sin
α
tw
∙
(1 +
k
00
12
) (1
−
k
0
21
)
−
(1
−
k
0
12
) (1 +
k
00
21
)
(1
−
k
00
0
) (1
−
k
0
21
) + (1 +
k
0
0
) (1 +
k
00
21
)
−
(38)
10 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2014. № 3