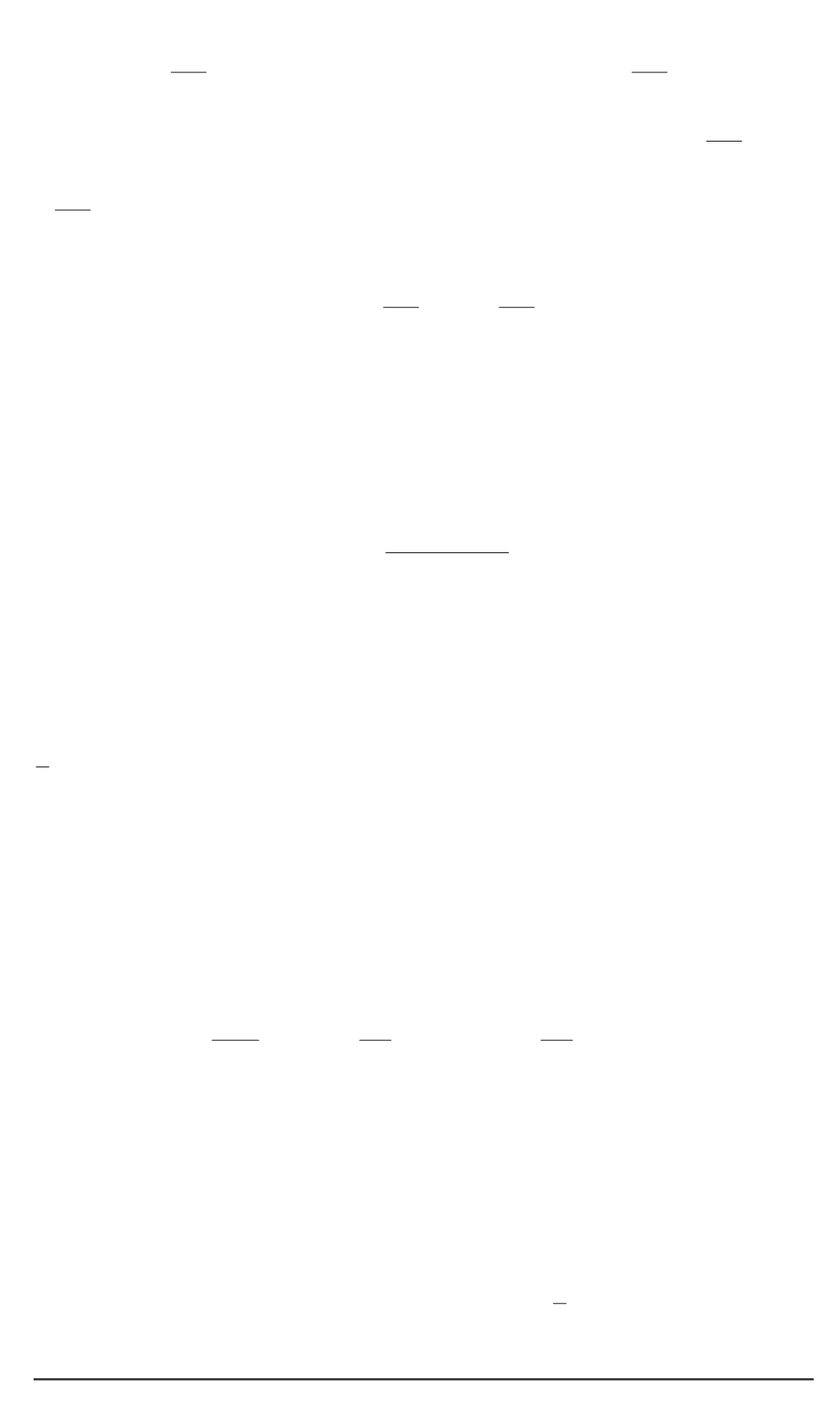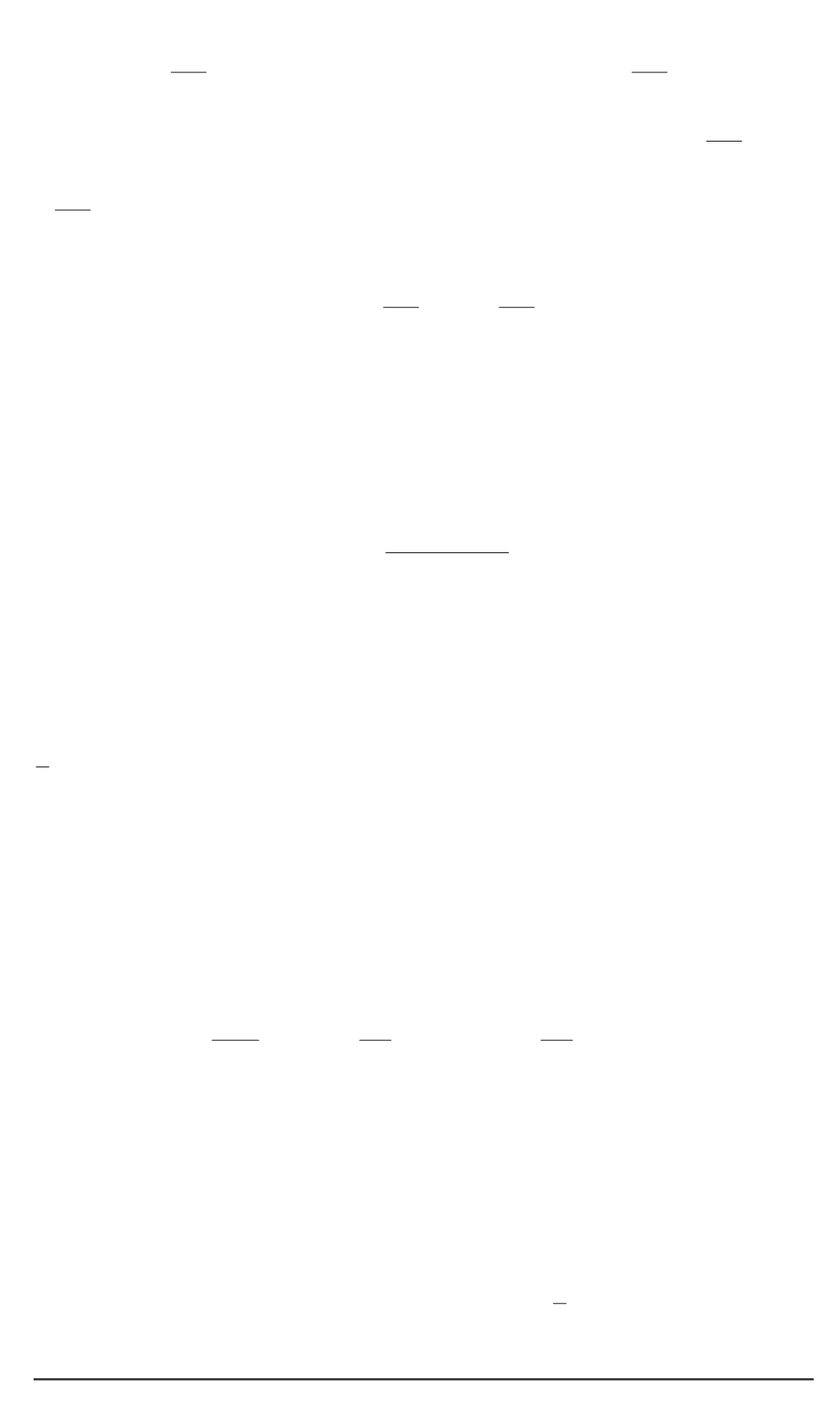
+
R
(
Ind
)
∂Y
∂ξ
i,j
[
ξ
−
ξ
i,j
]
,
Y
(
η
) =
Y
i,j
+
R
(
Ind
)
∂Y
∂η
i,j
[
η
−
η
i,j
]
;
здесь
R
(
Ind
)
— ограничитель значений производных
∂Y
∂ξ
i,j
и
∂Y
∂η
i,j
.
Входящие в кусочно-линейные распределения
Y
(
ξ
)
, Y
(
η
)
про-
странственные производные
∂Y
∂ξ
i,j
,
∂Y
∂η
i,j
вычисляются следу-
ющим образом.
1. Сначала для дискретной функции
Y
i
определим приближенное
значение
F
i
первой частной производной по пространственной пере-
менной
ξ
или
η
с шестым (четвертым) порядком точности.
Для этого найдем первую производную
f
по переменной
ξ
или
η
по обычной аппроксимационной формуле второго порядка точности
f
i
=
Y
i
+1
−
Y
i
−
1
2Δ
,
где
Δ
— шаг пространственной сетки в направлении
ξ
или
η
. То-
гда приближенное значение первой производной
F
i
получается из
решения системы уравнений с трехдиагональной матрицей. Эта ли-
нейная система уравнений представляет собой компактную схему для
нахождения первой производной с четвертым порядком точности:
1
6
(
F
i
+1
+ 4
F
i
+
F
i
−
1
) =
f
i
.
Важно отметить, что данная компактная схема имеет меньший ко-
эффициент при ошибке аппроксимации порядка
O
(Δ
4
)
, чем обычная
схема четвертого порядка точности.
Для нахождения приближенного значения
F
i
первой частной про-
изводной по пространственным переменным
ξ
или
η
с ошибкой ап-
проксимации на уровне
O
(Δ
6
)
вычисления следует проводить по фор-
муле
F
i
=
1
12Δ
E
+
Δ
2
5
−
1
6
E
+
Δ
2
5
Δ
0
!
f
i
,
где
Δ
0
f
i
=
f
i
+1
−
f
i
−
1
,
Δ
2
f
i
=
f
i
+1
−
2
f
i
+
f
i
−
1
. Отметим, что приве-
денная формула является симметричной конечной разностью шестого
порядка точности [23].
Монотонизированные приближенные значения
F
∗
i
первой част-
ной производной определяются на основе следующих соотноше-
ний:
F
∗
i
= minmod
F
R
i
, F
L
i
, где
F
R
i
= minmod (
F
i
+1
, F
i
)
и
F
L
i
=
= min mod(
F
i
, F
i
−
1
)
,
min mod (
a, b
) =
1
2
(
sign
(
a
) +
sign
(
b
))
×
×
min (
|
a
|
,
|
b
|
)
;
56 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2009. № 4