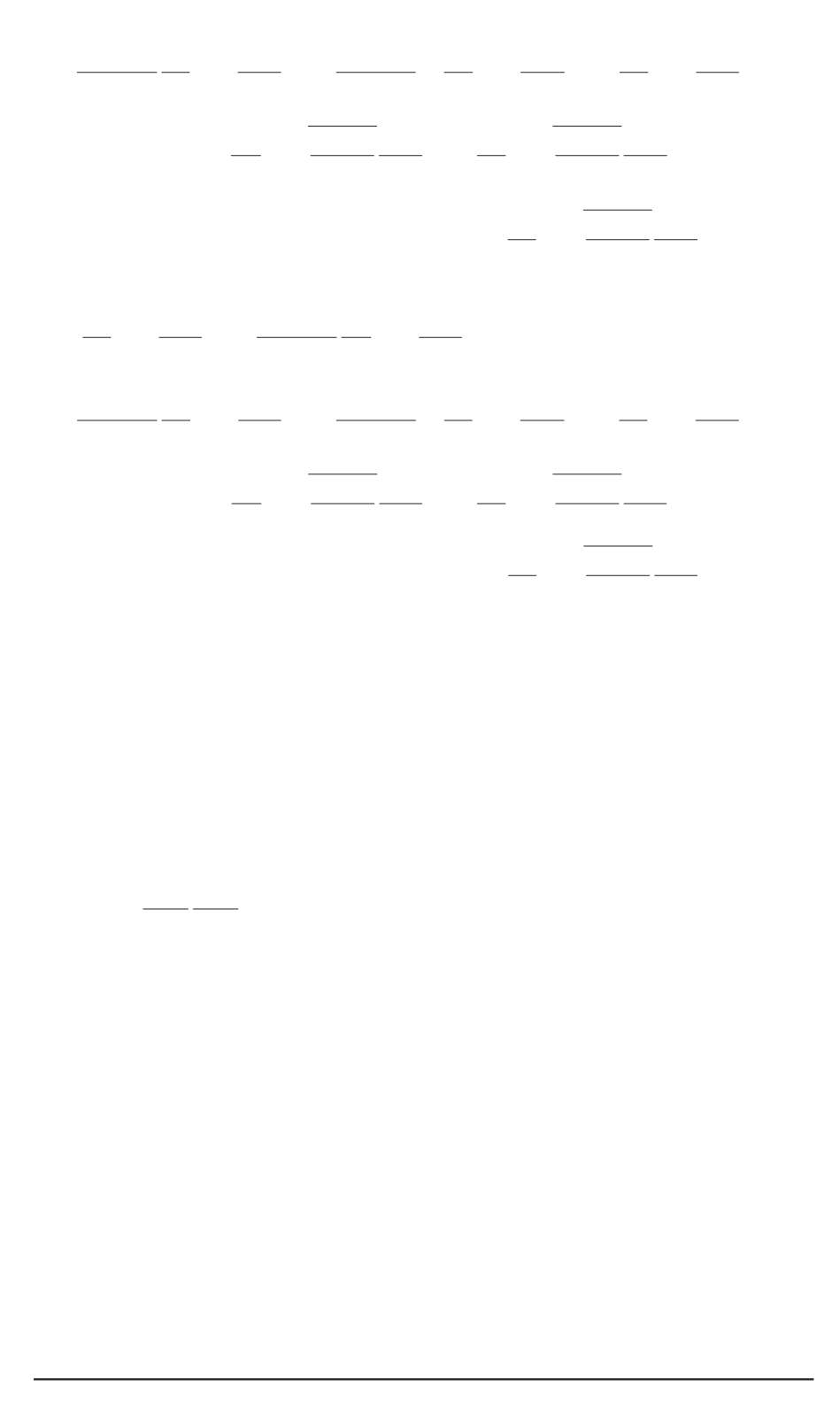
+
(1
−
σ
)
2
∂
∂z
F
∂U
y
∂z
+
(1 +
σ
)
2
∂
∂y
F
∂U
x
∂x
+
∂
∂y
F
∂U
z
∂z
+
+
k
opt
∂
∂x
g
22
g
33
g
11
∂U
y
∂x
+
∂
∂y
g
33
g
11
g
22
∂U
y
∂y
+
+
∂
∂z
g
11
g
22
g
33
∂U
y
∂z
= 0;
λ
z
∂
∂z
F
∂U
z
∂z
+
(1
−
σ
)
2
∂
∂x
F
∂U
z
∂x
+
+
(1
−
σ
)
2
∂
∂y
F
∂U
z
∂y
+
(1 +
σ
)
2
∂
∂z
F
∂U
x
∂x
+
∂
∂z
F
∂U
y
∂y
+
+
k
opt
∂
∂x
g
22
g
33
g
11
∂U
z
∂x
+
∂
∂y
g
33
g
11
g
22
∂U
z
∂y
+
+
∂
∂z
g
11
g
22
g
33
∂U
z
∂z
= 0
.
Здесь принято, что все коэффициенты, входящие в данную систему
уравнений, равны между собой
F
= (
∇
f,
∇
f
)
α
/2
+
ε
,
i
∈ {
x, y, z
}
.
Граничные условия, необходимые для решения данной системы урав-
нений, задаются следующим образом:
U
i
|
Г
=
r
∗
i
|
∂
(
A B F E D C G H
)
−
r
i
|
∂
(
ABFEDCGH
)
, i
∈ {
x, y, z
}
.
Компоненты ковариантного метрического тензора, входящие в систе-
му уравнений, определяются с помощью соотношений
g
ik
=
3
α
=1
∂r
α
∂q
i
∂r
α
∂q
k
, g
kj
=
δ
j
i
=
1
, i
=
j
0
, i
=
j
, q
1
=
x, q
2
=
y, q
3
=
z.
При этом
f
является функцией, управляющей адаптацией расчетных
узлов, коэффициент
α
задает необходимую степень сгущения узлов
расчетной сетки, коэффициенты
λ
i
>
0
и
σ
∈
[
−
1
,
1]
.
Параметр
ε
≈
min
h
i
∈
A B F E D C G H
(
h
i
)
выбирается как величина,
имеющая ненулевое значение, и порядка шага сетки
h
, чтобы избе-
жать особенности в тех узлах, где
∇
f
= 0
. Для численного решения
уравнений, применяемых для построения регулярных адаптивных
сеток, представленных в операторной форме
AU
= 0
, используется
модифицированный вариант итерационного метода вариационного
типа — метод минимальных невязок [10]. Здесь отметим также, что,
при применении многоблочной технологии расчетов, рассматрива-
емая численная методика позволяет построить квазиортогональные
структурированные сетки в областях сложной формы.
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2009. № 4 47