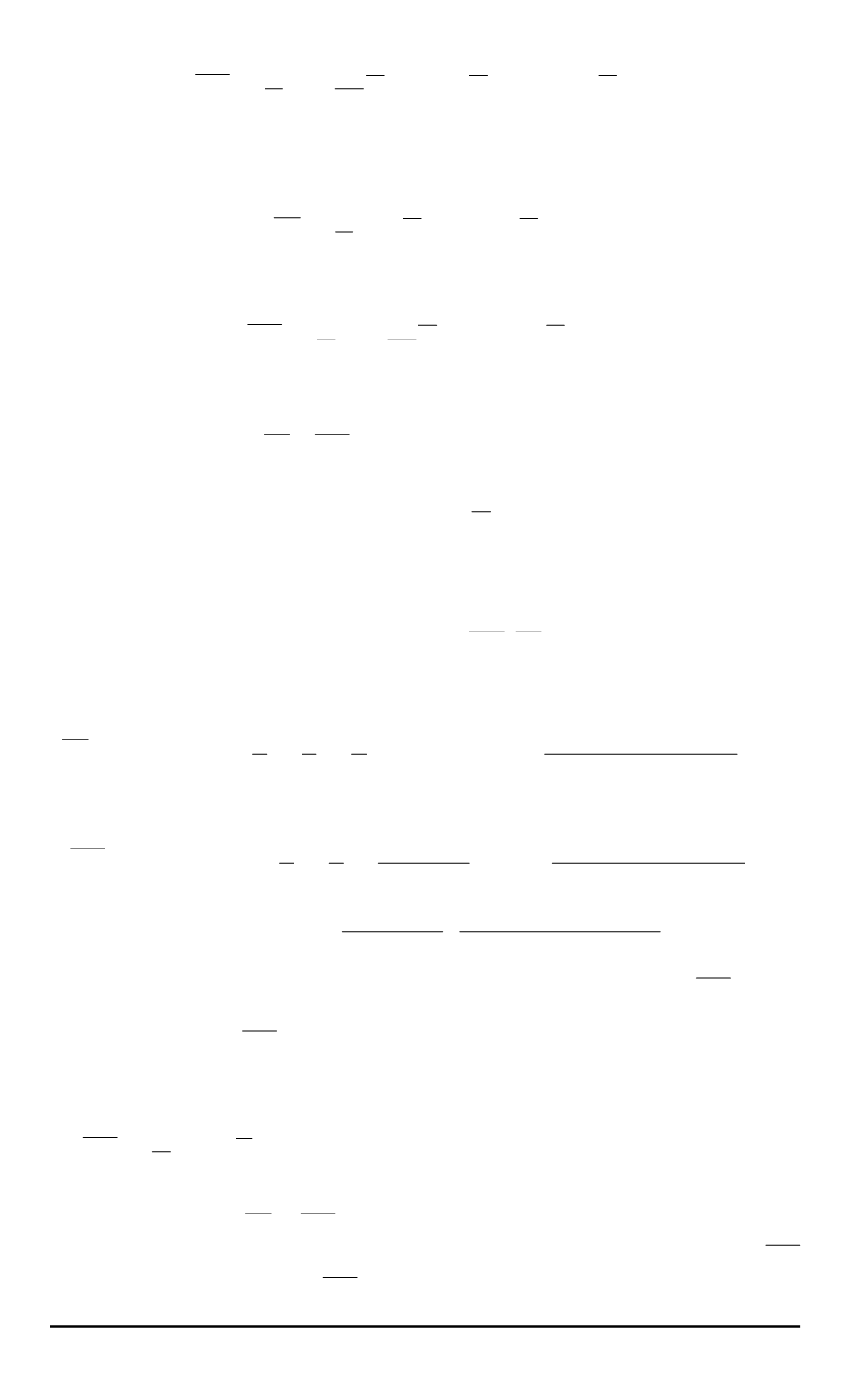
P
эм
=
1
T
ϑT
Z
0
e
вр
U
i
1
dt
+
T
Z
ϑT
εi
2
dt
+
T
+
T
p
Z
T
εi
3
dt
)
,
(17)
а для расширенной коммутации
P
п
=
1
T
ϑT
Z
0
i
1
dt
+
T
+
ϑT
Z
ϑT
i
2
dt
);
(18)
P
эм
≈
1
T
ϑT
Z
0
e
вр
U
i
1
dt
+
T
+
ϑT
Z
ϑT
εi
2
dt
)
.
(19)
На основе формул (16)–(19) с учетом формул (1), (2), (7)–(15) полу-
чим выражения для
P
п
и
P
эм
применительно к благоприятному случаю
(cм. рис. 3)
i
1
(
ϑT
) = (
U
−
E
)
/R, i
1
(
ϑT
) = 1
−
ε,
(20)
которому соответствует максимальное значение электромагнитного
КПД. Такой КПД можно представить отношением
η
эм
=
P
эм
/P
п
=
P
эм
/P
п
.
(21)
Для криволинейной ЭДС получим
P
п
= (1
−
ε
) 1
−
ϑ
2
±
ϑ
2
−
1
β
+ (1 +
aε
)
ϑ
−
(1 +
a
)
ε
(1
−
e
−
rϑ
)
r
;
(22)
P
эм
=
ε
(1
−
ε
)
h
1
−
ϑ
2
±
ϑ
2
+
ar
+
β
β
(
r
−
β
)
i
+
aε
h
ε
(1 +
a
)(1
−
e
−
rϑ
)
r
−
−
(1 +
aε
)
ϑ
i
+
(1 +
a
)
βε
r
(
r
−
β
)
h
(1 +
a
)
ε
(1
−
e
−
2
rϑ
)
2
−
−
(1 +
aε
)(1
−
e
−
rϑ
)
i
+ Δ
P
эм
.
(23)
Здесь и далее:
Δ
P
эм
— относительная электромагнитная мощность,
развиваемая на третьем интервале; для обычной коммутации
Δ
P
эм
=
1
T
T
+
T
p
Z
T
εi
з
dt
=
ε
{
1
−
ε
−
(
ε
+
ε
p
) ln[(1 +
ε
p
)
/
(
ε
+
ε
p
)]
}
/β,
(24)
а в формулах для
P
п
и
P
эм
следует брать знак минус
(
−
)
; для расши-
ренной коммутации следует брать знак плюс
(+)
, а мощностью
Δ
P
эм
можно пренебречь, т.е.
Δ
P
эм
≈
0
.
52 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2007. № 3