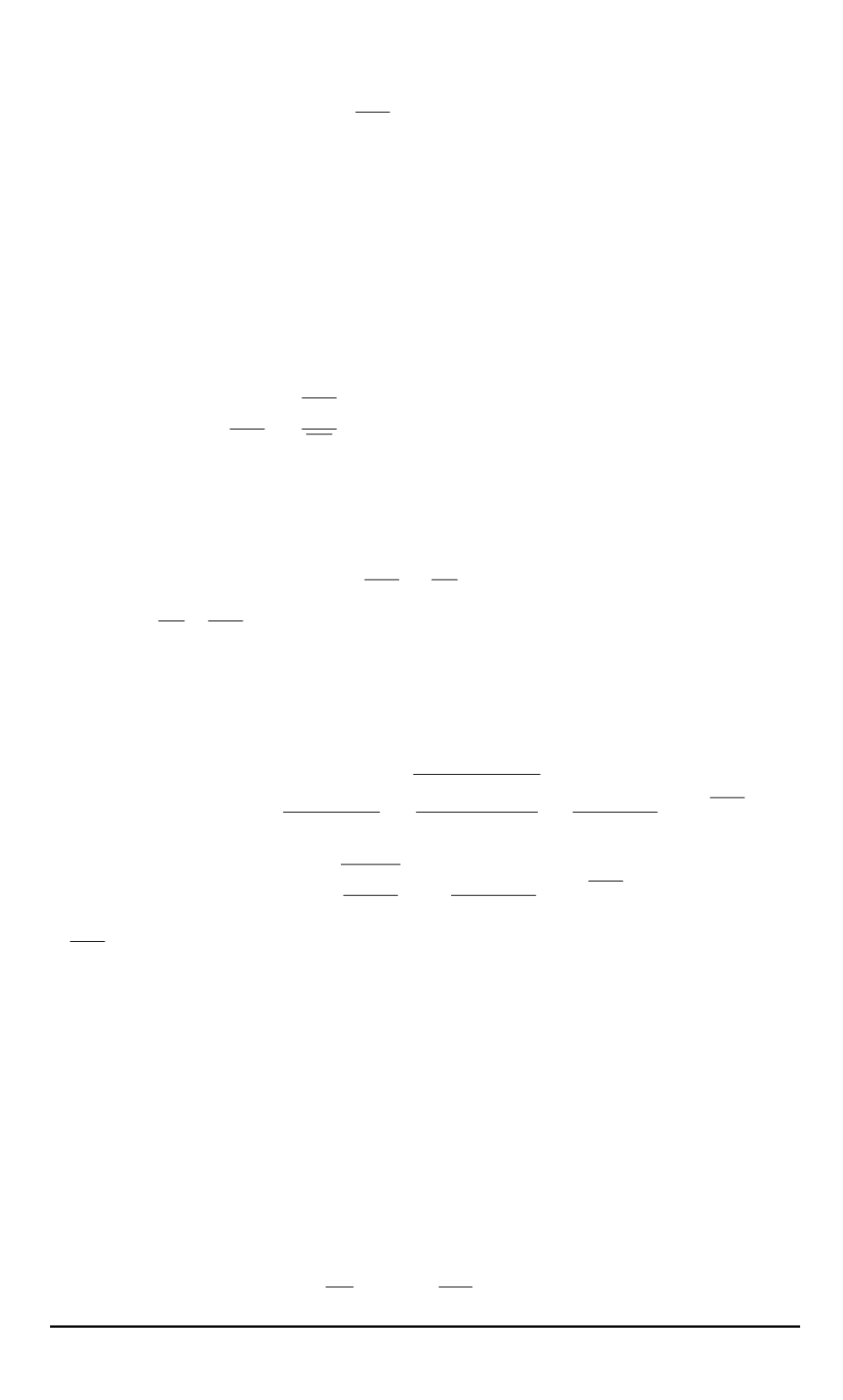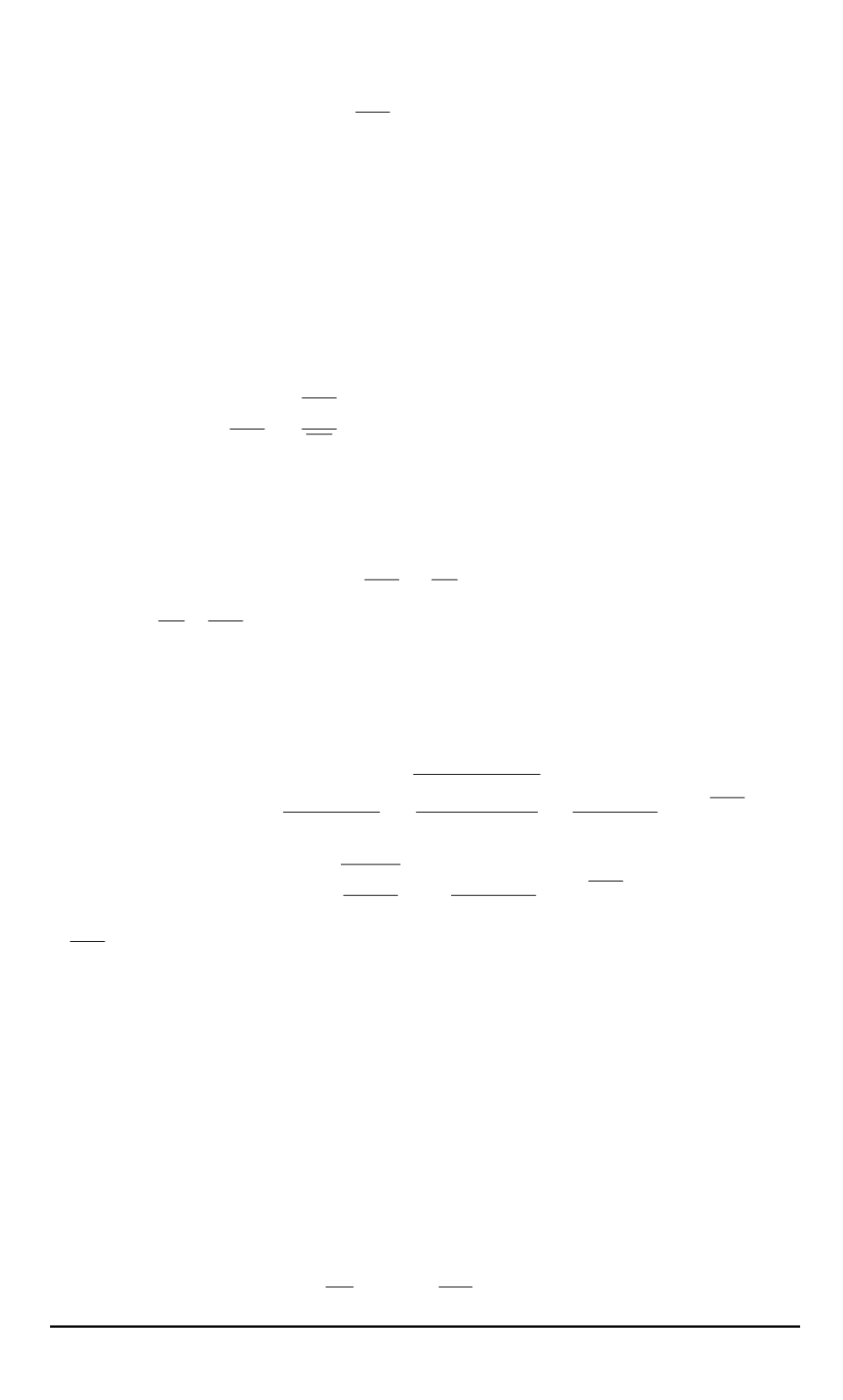
несколько меньшей номинальной мощности
P
2н
, причем
γ
=
P
2
P
2н
≈
0
,
75
. . .
0
,
9
.
Известно, что КПД — максимален при равенстве мощности элек-
трических (омических) потерь (переменных, пропорциональных
γ
2
)
и
мощности неэлектрических потерь
P
мг
+
P
мех
(примерно постоянных),
т.е. при равенстве
(
P
п
−
P
эм
)
γ
2
=
P
эм
−
P
2н
,
P
п
и
P
эм
относятся к номинальному режиму работы двигателя.
Из последнего равенства с учетом (46) легко получить другое ра-
венство
P
эм
P
п
=
P
эм
P
п
= (
η
н
+
γ
2
)
/
(1 +
γ
2
) =
C
;
η
н
=
<
η
дн
.
Для БДПТ с дискретным управлением значения
ε
и
ϑ
нужно опре-
делять путем решения системы двух уравнений. Первое уравнение
P
эм
=
P
п
С
,
в котором
P
п
и
P
эм
представляют собой полученные ранее соответству-
ющие выражения, а второе уравнение — (35) или (36). Если исполь-
зовать приближенные выражения (39), (31) и (37), (40), (31) и (38),
то получим для криволинейной и прямолинейной ЭДС уравнения с
одним неизвестным —
ε
:
ε
−
C
+ [
±
(
ε
−
C
) +
rε
(1
−
ε
)
6
β
0
]
s
1
−
ε
2
r
(1 +
a
)
β
0
−
ε
(1
−
ε
)
3
β
0
+ Δ
P
эм
= 0;
(
ε
−
C
) 1
±
r
1
−
ε
2
bβ
0
−
ε
(1
−
ε
)
3
β
0
+ Δ
P
эм
= 0;
Δ
P
эм
можно определить по формулам (24) и (32).
Для БДПТ с непрерывным управлением следует сначала опреде-
лить значение коэффициента
ε
из биквадратного уравнения
(
c
2
−
a
2
b
)
ε
4
−
(
b
−
2
cd
)
ε
2
+
d
2
= 0
,
(47)
а затем определить значение угла
Θ
по формуле
Θ = arctg(
a ε
)
,
(48)
где
a
= (1
−
η
)
ρ/
(1 +
η
)
,
b
= [2(1 +
η
)(1
−
ρ
2
η
)]
2
,
c
=
ρ
2
(1
−
6
η
+
η
2
)
,
d
= (1 +
η
)
2
,
η
=
η
н
=
η
дн
<
.
Формулы (47) и (48) получены, исходя из системы уравнений
∂η
∂ε
= 0
,
∂η
∂
Θ
= 0
.
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2007. № 3 57