Применяя выражение (46) для
η
и считая, что
P
мг
+
P
мех
≈
const,
получим систему двух уравнений с неизвестными
ε
и
Θ
:
∂P
эм
∂ε
=
η
∂P
п
∂ε
,
∂P
эм
∂
Θ
=
η
∂P
п
∂
Θ
.
Учитывая выражения (41) и (42), получим после взятия производных
и последующих преобразований
2
ρε
sin Θ + cos Θ
−
ρ
2
ε
2
cos Θ
−
2
ε
=
=
η
(2
ρε
sin Θ
−
cos Θ +
ρ
2
ε
2
cos Θ
−
2
ρ
2
ε
)
.
(49)
Разделив обе части уравнения (49) на
cos Θ
и учитывая выражения
(48) и
cos Θ = 1
/
p
1 + tg
2
Θ
, после преобразований получим уравне-
ние (47). Из формулы (48) видно, что угол
Θ
тем больше, чем больше
ρ
,
ε
и меньше
η
.
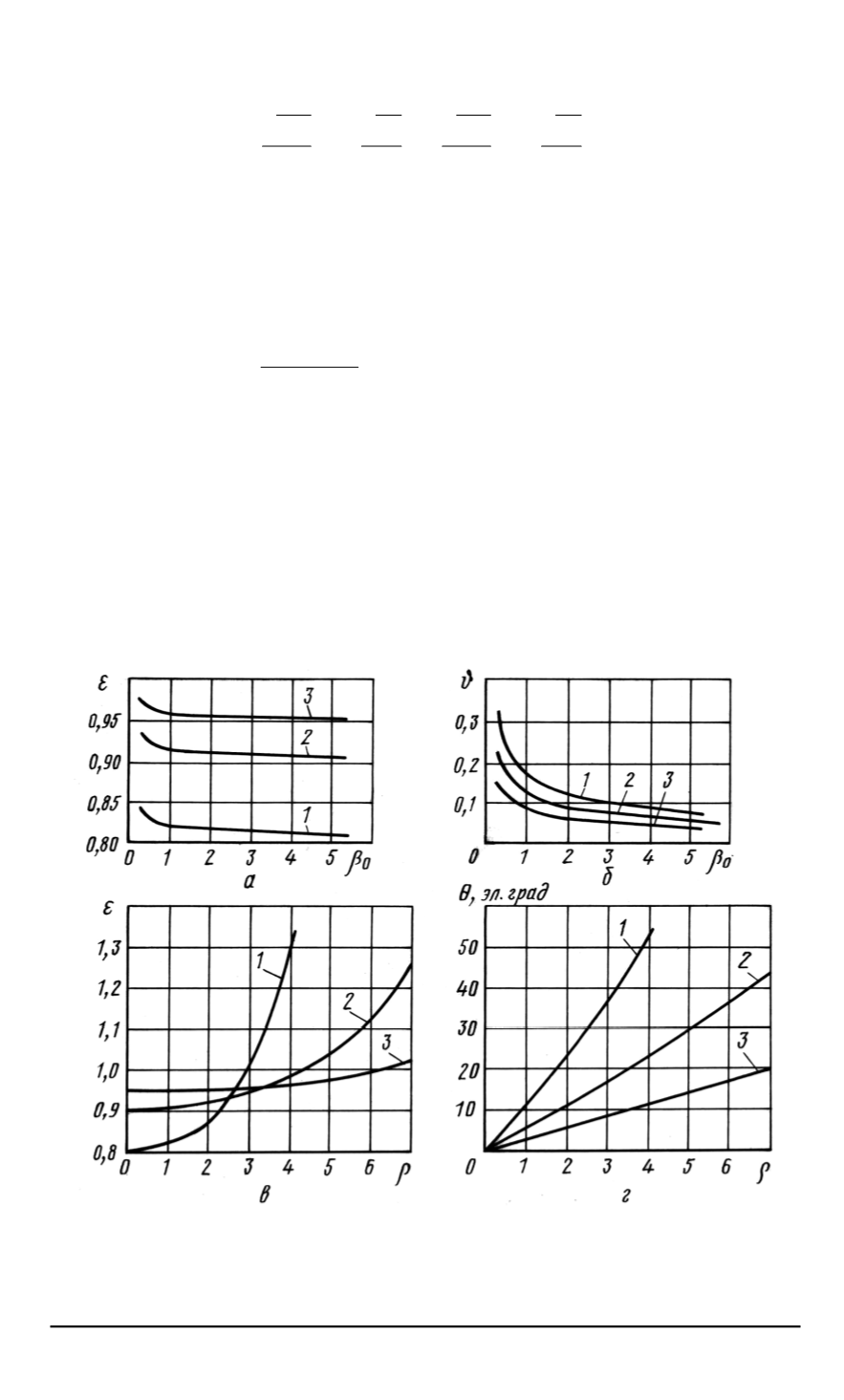
На рис. 4,
а, б
приведены графические зависимости оптимальных
значений коэффициента ЭДС
ε
и относительного угла
ϑ
от значений
характеристики якорной обмотки
β
0
для трех значений КПД
η
при-
менительно к БДПТ с дискретным управлением и расширенной ком-
мутацией. Из рис. 4,
а, б
видно, что чем больше
η
, тем больше
ε
, но
меньше
ϑ
.
Рис. 4. Оптимальные значения коэффициента ЭДС
ε
и относительного угла
ϑ
для БДПТ с дискретным управлением (
а
и
б
соответственно); коэффициента
ЭДС
ε
и угла
Θ
для БДПТ с непрерывным управлением (
в
и
г
соответственно)
при
η
= 0
,
6
(
1
); 0,8 (
2
); 0,9 (
3
)
58 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2007. № 3


