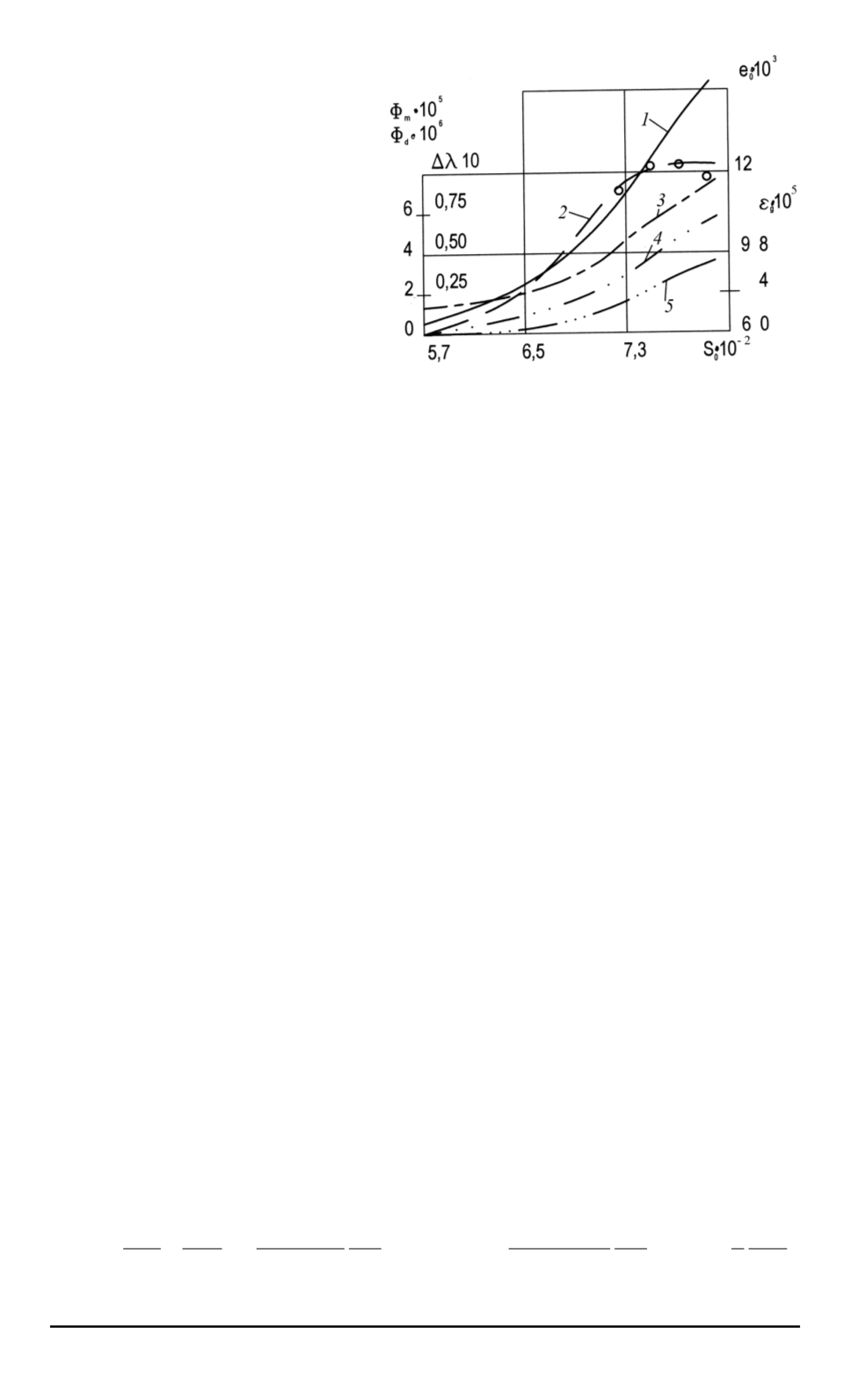
Рис. 2. Зависимость
Δ
λ
,
Q
m
,
Φ
d
,
e
0
и
ε
p
от
интенсивности напряжений
S
0
разница коэффициентов по-
перечной деформации превы-
шает 17%. Описанная мето-
дика позволяет провести по-
добный анализ и на других
уровнях
S
0
=
const. На рис. 2
для
θ
=
π/
6
представлены
кривые
1, 2, 3, 4
для
e
0
,
Δ
λ
,
Φ
m
,
Φ
d
соответственно,
показывающие их зависимо-
сти от интенсивности напря-
жений
S
0
. Кривая
5
относится
к деформации разрыхления:
ε
p
=
ε
0
−
ε
ν
, где
ε
0
= (
ε
t
+
+
ε
z
+
ε
r
)
/
3
,
ε
ν
=
σ
0
/
3
K
. Эта кривая указывает на то, что в процессе
развития анизотропии деформация разрыхления может иметь место.
Все кривые являются явно возрастающими, кроме кривой
2
для
Δ
λ
, на которой наблюдается (с приближением к предельному напря-
жению) стабилизация значения. Подобное поведение можно заметить
[5] у образцов с непропорциональным нагружением, для которых на
диаграмме
λ
ε
–
λ
σ
видно, что разница
Δ
λ
остается примерно неизмен-
ной при возрастающей пластической деформации.
Полученные результаты расчетов табл. 2 и графики на рис. 2 под-
тверждают наличие эффектов анизотропии и разрыхления, а высокие
значения для
ν
12
и
ν
21
находятся в согласии с результатами иссле-
дований, отмеченных в работе [4]. Далее приведена математическая
модель, в основе которой положены уравнения (1) и (7).
Функциональная зависимость обобщенных характеристик от инва-
риантов тензора напряжений обусловлена выбором конкретного вида
потенциала деформаций, а именно учетом зависимости нелинейной
деформации как от
S
0
и
θ
, так и среднего напряжения
σ
0
[8]:
Φ =
σ
2
0
/
2
K
+
S
2
0
/
6
μ
+
g
(
σ
0
, S
0
)
χ
(
θ
)
/
3
μ,
(14)
где
μ
и
K
— модули упругости при сдвиге и объемной деформации
соответственно
g
(
σ
0
, S
0
)
и
χ
(
θ
)
-функции.
Первая представляется выражением
g
(
σ
0
, S
0
) =
b
0
(
S
0
+
c
0
σ
0
)
2
S
m
0
/m
=
b
0
C
2
н
S
m
+2
0
/m,
(15)
а вторая — в виде
χ
(
θ
) = 1 +
aη
, где
С
н
= (1 +
c
0
ξ
)
;
a, b
0
,
c
0
,
m
—
постоянные величины.
Пользуясь дифференциальными соотношениями
Φ
m
=
1
3
S
0
∂
Φ
∂S
0
+
η
S
0
sin 3
θ
∂
Φ
∂θ
,
Φ
d
=
−
9
2
S
2
0
sin 3
θ
∂
Φ
∂θ
, ε
0
=
1
3
∂
Φ
∂σ
0
,
(16)
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2007. № 1 51


