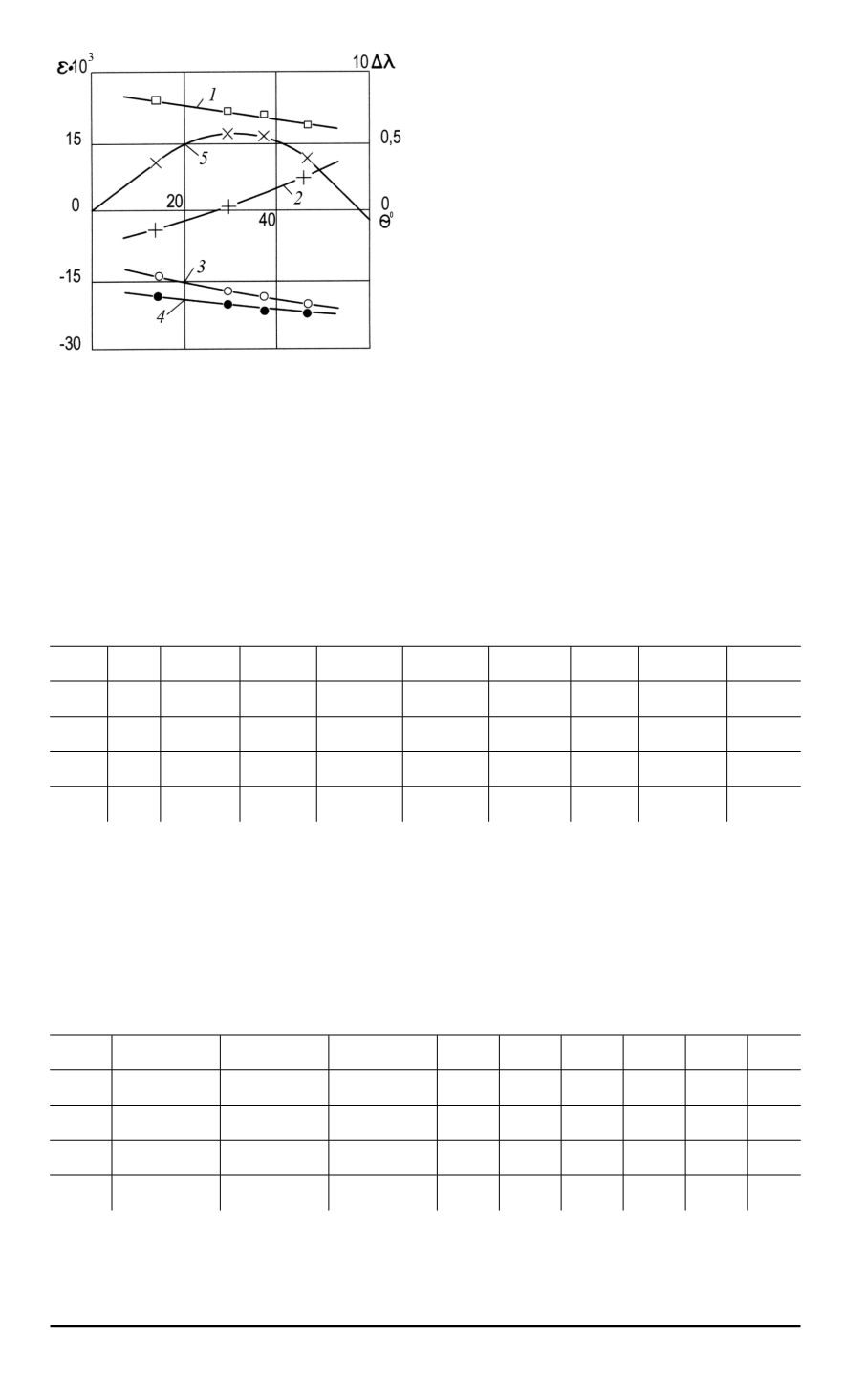
Рис. 1. Зависимость деформаций и
разницы параметров Лоде от угла
θ
радиальную деформацию
ε
r
= [2
ε
z
−
ε
t
(1 +
λ
ε
)]
/
(1
−
λ
ε
)
,
которую определяют из исходной
формулы для параметра
λ
ε
. За-
тем повторяются вычисления
B
i
,
Φ
m
,
Φ
d
.
На этих итерациях
Φ
d
и
Φ
m
уже
не осредняются. Различие значе-
ний
ε
r
на третьей и четвертой ите-
рациях составляет менее 2%. Та-
ким образом, методика, опираясь
на выводы (9) и (10), вытекающие
из уравнений (1), использует ре-
зультаты испытаний группы образцов при совместной их обработке.
На рис. 1 показаны кривые
1, 2, 3
и
4
для деформаций соответ-
ственно
ε
t
,
ε
z
,
ε
r
и
ε
a
r
, а также кривая
5
для
Δ
λ
, иллюстрирующие
зависимость этих величин от
θ
. В табл. 1 приведены исходные данные
и результаты расчетов при
S
0
= 780
МПа.
Таблица 1
θ
◦
σ
t
ε
t
,
∙
10
3
ε
z
∙
10
3
ε
r
∙
10
3
ε
a
r
∙
10
3
λ
ε
Δ
λ
Φ
m
∙
10
5
Φ
d
∙
10
6
13,9 865 24,7 – 3,7 – 14,24 – 18,99 – 0,553 0,053 8,25 5,44
30 901 21,6 0,9 – 17,64 – 19,98 – 0,087 0,087 8,46
6,4
36,6 895 21,1 3,5 – 19,88 – 21,94 0,123 0,077 9,07 6,28
46,1 865 18,3 7,5 – 21,17 – 22,98 0,440 0,060 9,15 6,44
Найденные значения характеристик
Φ
m
и
Φ
d
дают возможность
оценить анизотропию, возникающую в ходе пластической деформа-
ции при
Φ
k
=
K
−
1
и
æ = 0
по соотношениям (8) и (9). Результаты
представлены в табл. 2.
Таблица 2
θ
◦
E
1
∙
10
−
4
E
2
∙
10
−
4
E
3
∙
10
−
4
ν
12
ν
21
ν
13
ν
31
ν
23
ν
32
13,9 3,60
3,60
3,66 0,48 0,50 0,46 0,49 0,43 0,44
30
3,33
3,47
3,63 0,49 0,51 0,45 0,49 0,42 0,44
36,6 3,14
3,22
3,38 0,49 0,51 0,45 0,48 0,43 0,45
46,1 3,11
3,17
3,36 0,50 0,51 0,44 0,48 0,43 0,46
Из табл. 2 видно, что наибольшая разница секущих модулей
упругости по разным направлениям составляет 5. . . 6%, тогда как
50 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2007. № 1


