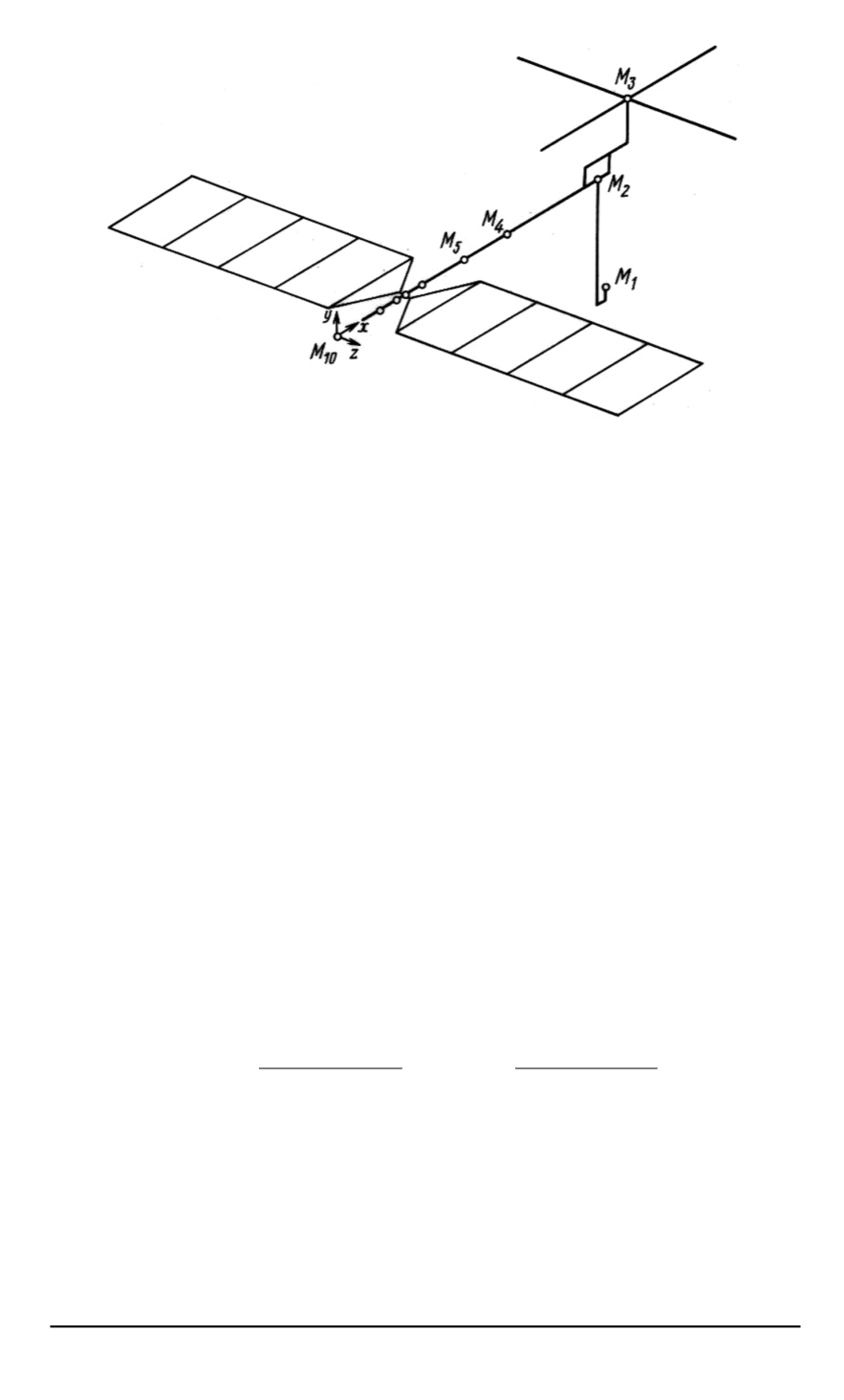
Рис. 1. Рис. 1. Конечно-элементная модель космического аппарата:
—— — балоч-
ные элементы;
◦
— сосредоточенные массы
реального космического летательного аппарата, состоящая из балоч-
ных элементов с упругими связями и сосредоточенными массами (см.
рис. 1). Модель имеет 2478 степеней свободы и 139 параметров.
По всем параметрам были вычислены функции чувствительности
первого и второго порядков для низших пяти тонов упругих колеба-
ний модели. На рис. 2,
а
и
б
изображены безразмерные и нормиро-
ванные относительно наибольших значений величины функций чув-
ствительности (“столбики”) первого порядка для собственных чисел
(см. рис. 2,
а
) и норм собственных векторов (см. рис. 3,
б
) для группы
наиболее влияющих параметров. Такие диаграммы удобно использо-
вать для анализа иерархии влияния в первом приближении вариаций
параметров на исследуемые динамические характеристики.
На рис. 3,
а
и
б
показана сходимость сумм в разложениях (9) и (16)
для первых пяти тонов в зависимости от количества слагаемых. Для
примера выбраны векторы чувствительности для наиболее влияющего
параметра. По вертикальным осям отложены относительные ошибки
следующего вида:
Δ
1
k
=
k
˜
Q
(
k
)
h
−
Q
(
k
)
h
k
k
˜
Q
(
k
)
h
k
; Δ
2
k
=
k
˜
R
(
k
)
hh
−
R
(
k
)
hh
k
k
˜
R
(
k
)
hh
k
,
где
˜
Q
(
k
)
h
,
˜
R
(
k
)
hh
— точные значения функций чувствительности векторов;
h
— номер наиболее влияющего параметра.
Для всех других векторов чувствительности картины сходимости
аналогичны.
На рис. 4 приведены оценки точности разложений (4) для рассма-
триваемого примера. При этом совместно варьировались два наиболее
42 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2007. № 1


