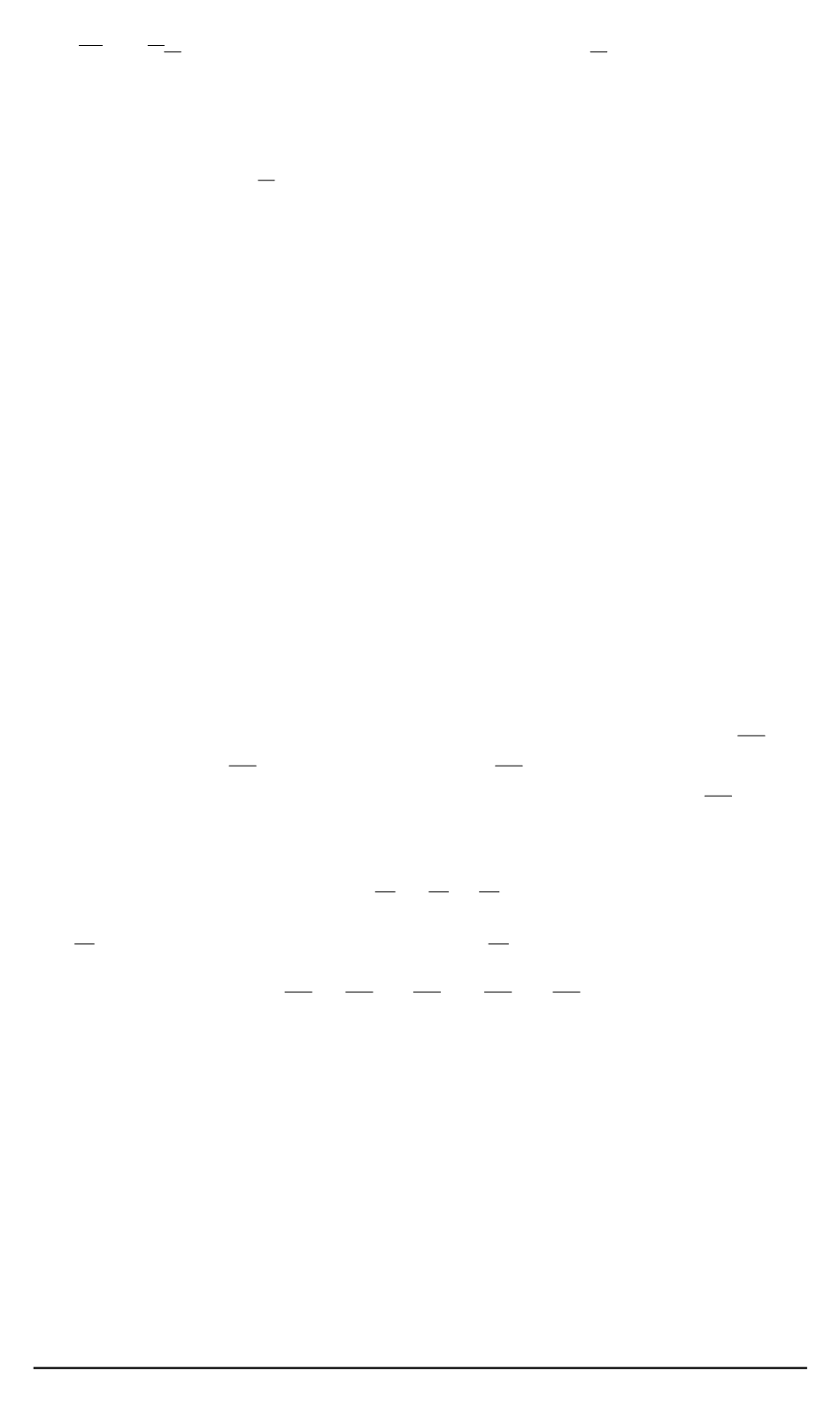
где
K
=
Jω
— вектор кинетического момента;
ω
= [
ω
x
, ω
y
, ω
z
]
т
—
вектор угловой скорости вращения КБ.
Тензор инерции КБ можно записать как
J
=
J
x
−
J
xy
−
J
xz
−
J
yx
J
y
−
J
yz
−
J
zx
−
J
zy
J
z
.
Уравнение вращательного движения в проекциях на оси связанной
системы координат имеет вид:
J
x
˙
ω
x
−
J
xy
˙
ω
y
−
J
xz
˙
ω
z
−
J
zx
ω
x
ω
y
−
J
zy
ω
2
y
−
J
z
ω
y
ω
z
+
+
J
yx
ω
x
ω
z
−
J
y
ω
y
ω
z
+
J
yz
ω
2
z
=
P
M
x
;
−
J
yx
˙
ω
x
+
J
y
˙
ω
y
−
J
yz
˙
ω
z
+
J
x
ω
x
ω
z
−
J
xy
ω
y
ω
z
−
J
xz
ω
2
z
+
+
J
zx
ω
2
x
+
J
zy
ω
x
ω
y
−
J
z
ω
x
ω
z
=
P
M
y
;
−
J
zx
˙
ω
x
−
J
zy
˙
ω
y
+
J
z
˙
ω
z
−
J
yx
ω
2
x
+
J
y
ω
x
ω
y
−
J
yz
ω
x
ω
z
−
−
J
x
ω
x
ω
y
+
J
xy
ω
2
y
+
J
xz
ω
y
ω
z
=
P
M
z
,
где
M
x
, M
y
, M
z
— проекции действующих моментов на оси связанной
системы координат.
При построении математической модели вращательного движения
используем силы тяжести и сопротивления, а также аэродинамиче-
скую подъемную силу; аэродинамические стабилизирующий (
M
δ
) и
демпфирующий (
M
ω
) моменты, момент
M
g
, вызванный смещением
центра масс КБ от оси нулевой подъемной силы, и момент
M
o
аэро-
динамической несимметрии.
Таким образом,
X
F
=
R
+
Q,
где
R
— вектор аэродинамической силы;
Q
— вектор силы тяжести;
X
M
=
M
δ
+
M
ω
+
M
g
+
M
o
.
Аэродинамические коэффициенты осевой, нормальной и боковой
аэродинамических сил в соответствии с рис. 2 записываются следую-
щим образом:
C
x
=
C
x
(
α
π
, M
) ;
C
y
=
C
н
(
α
π
, M
) cos
ϕ
π
;
C
x
=
−
C
н
(
α
π
, M
) sin
ϕ
π
,
где
C
н
(
α
π
, M
) =
C
α
y
(
α
π
, M
)
α
π
— аэродинамический коэффициент
нормальной силы в плоскости сoпротивления.
Аэродинамические коэффициенты моментов тангажа и рыскания
имеют вид
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2008. № 3 43