Влияние ветрового воздействия на динамику движения корректируемых боеприпасов - page 4

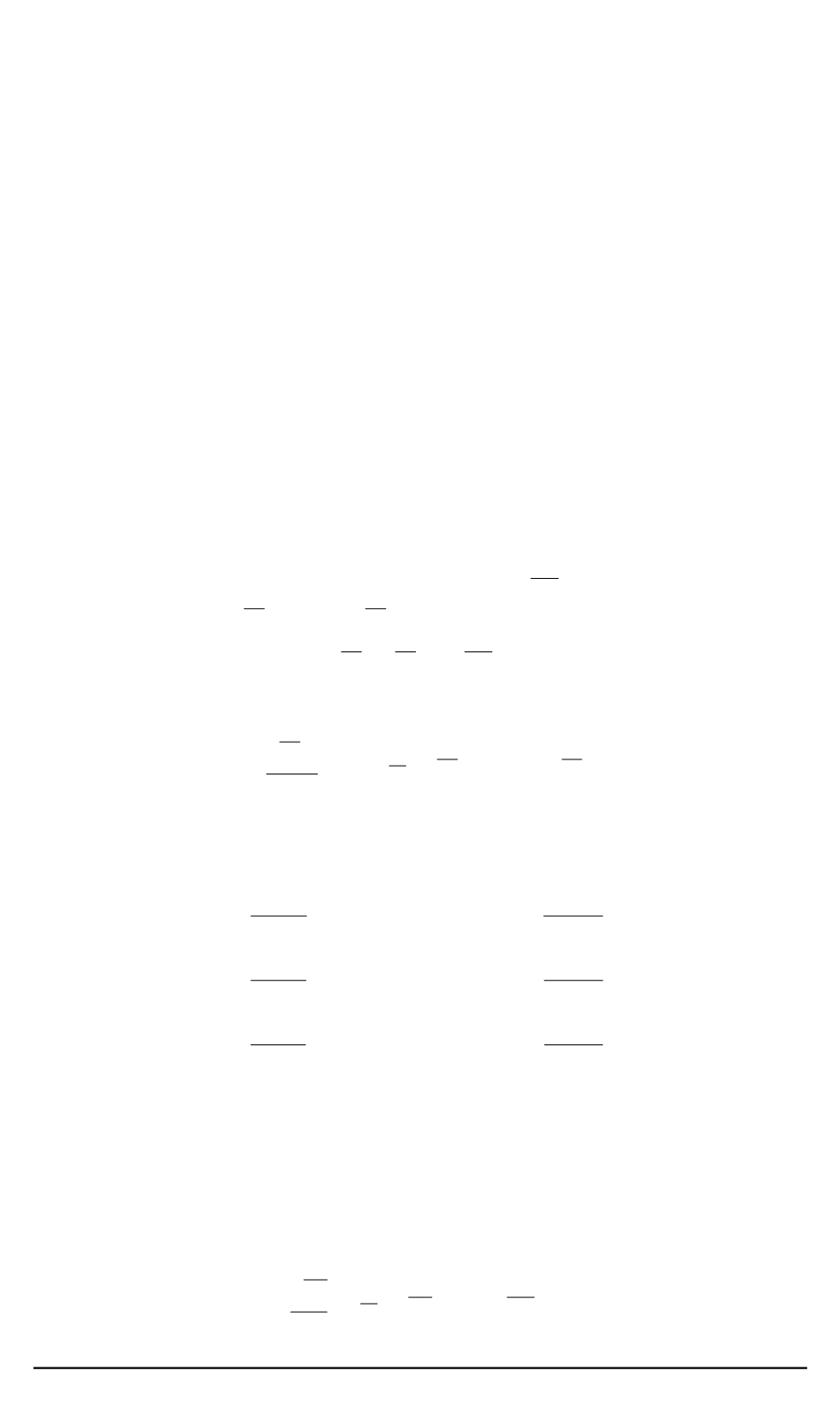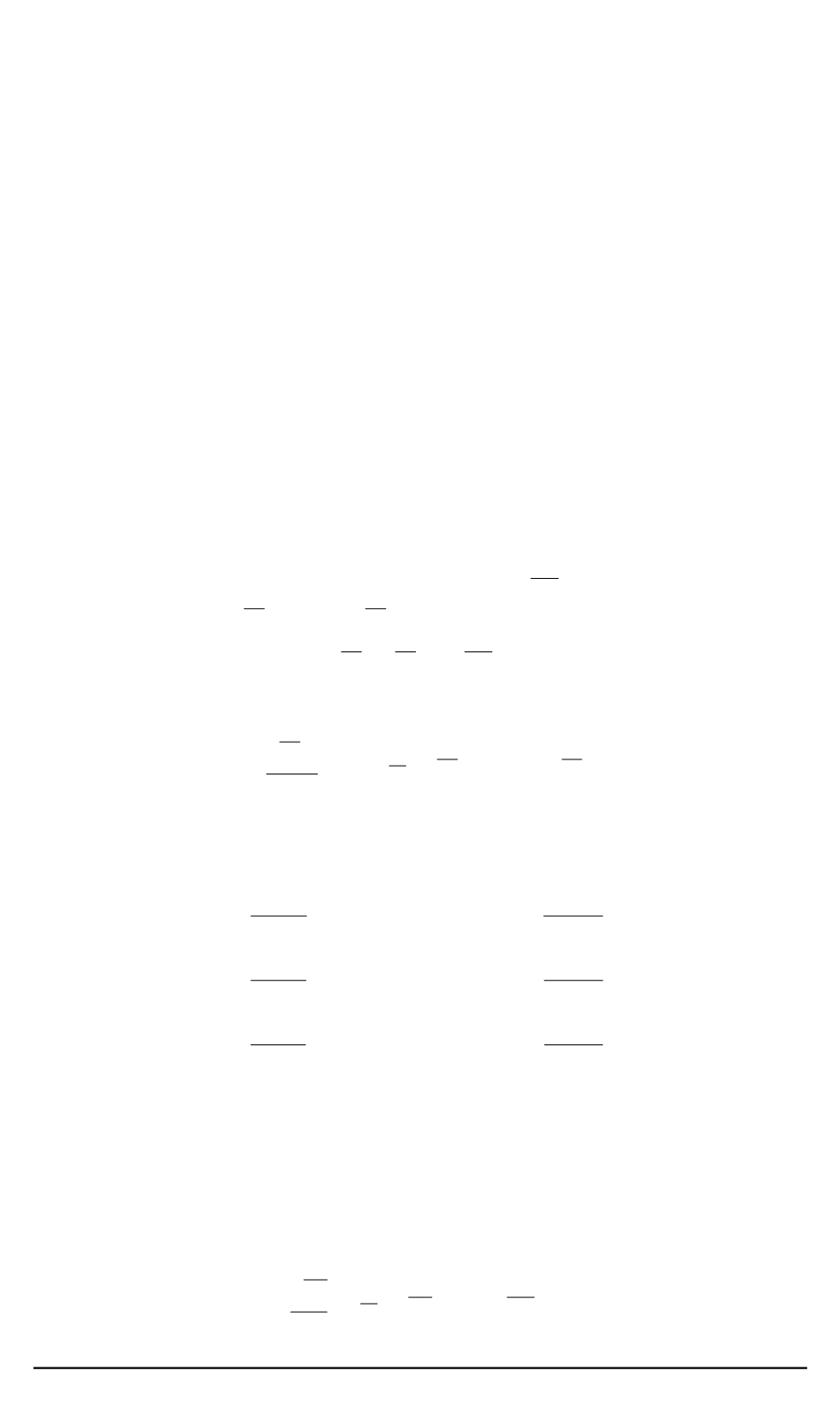
Cначала рассмотрим влияние ветра на динамику движения КБ на
неуправляемом участке траектории. Динамические уравнения записы-
ваются в проекциях на орты связанной системы координат. Уравнения
поступательного движения центра масс КБ записываются в проекциях
на орты нормальной земной (инерциальной) системы координат.
Для вектора в связанной системе координат (OXY Z ) можно запи-
сать  X
Y
Z  = A  Xин
Yин
Zин
 ,
где A — матрица перехода от инерциальной системы координат
( Xин Yин Zин ) к связанной,
A =
=
cos ϑ cos ψ sin ϑ − cos ϑ sin ψ
sin ψ sin γ − sin ϑ cos ψ cos γ cos ϑ cos γ cos ψ sin γ + sin ψ sin ϑ cos γ
sin ϑ cos ψ sin γ + sin ψ cos γ − cos ϑ sin γ cos ψ cos γ − sin γ sin ψ sin ϑ
(ψ, ϑ, γ — углы рыскания, тангажа и крена соответственно).
При наличии ветра, имеющего скорость W , скорости КБ относи-
тельно атмосферы V и земли V K связаны соотношением
V = V K − W.
Векторное уравнение поступательного движения имеет вид
m
dV K
dt
+ m ω × V K =
n Xj =1
F j .
В проекциях на оси связанной систем координат ( OXY Z ) получа-
ем  dVKx
dt
+ ωy VKz − ω zVKy = P Fx
m
;
dVKy
dt
+ ωz VKx − ω xVKz = P Fy
m
;
dVKz
dt
+ ωxVKy − ω y VKx = P Fz
m
,
где VKx , VKy, V Kz — проекции скорости центра масс КБ на оси свя-
занной систем координат; ωx , ωy , ω z — компоненты угловой скорости
вращения КБ по осям связанной системы координат; m, Fx, Fy , Fz —
масса КБ и проекции действующих сил по осям связанной системы
координат соответственно.
Уравнение вращательного движения имеет вид
dK
dt
+ ω × K =
m X
k =1
M k ,
42 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2008. № 3