и параметры которого определяются следующими уравнениями [3]:
dw
t
dt
=
−
V
L
T
w
t
+
σ
w
s
2
V
L
T
h
!
ε
h
(
t
) ;
dw
0
n
dt
=
w
n
+
σ
w
s
3
V
L
T
h
!
ε
h
(
t
) ;
dw
n
dt
=
−
V
L
T
2
w
0
n
−
2
V
L
T
w
n
+
+
σ
w
s
V
L
T
3
,
√
h
1
−
2
√
3
ε
h
(
t
) ;
ε
h
(
t
) =
ε
k
, t
2
[
kh,
(
k
+ 1)
h
] ;
ε
k
N
(0
,
1)
.
(2)
Такое представление случайного процесса ветровых порывов соот-
ветствует аппроксимации его гауссовым марковским случайным про-
цессом. Параметры
σ
w
и
L
T
зависят от условий атмосферной стра-
тификации (времени года или суток, облачности в приземном слое,
рельефа местности и т.д.). В работе [2] приведены результаты экспе-
риментальных исследований атмосферной турбулентности, согласно
которым
L
T
лежит в пределах от 150 до 1500. . . 2000 м, а
σ
w
— от 0,5
до 5 м/с.
Для нахождения решения к системе уравнений (2) требуется доба-
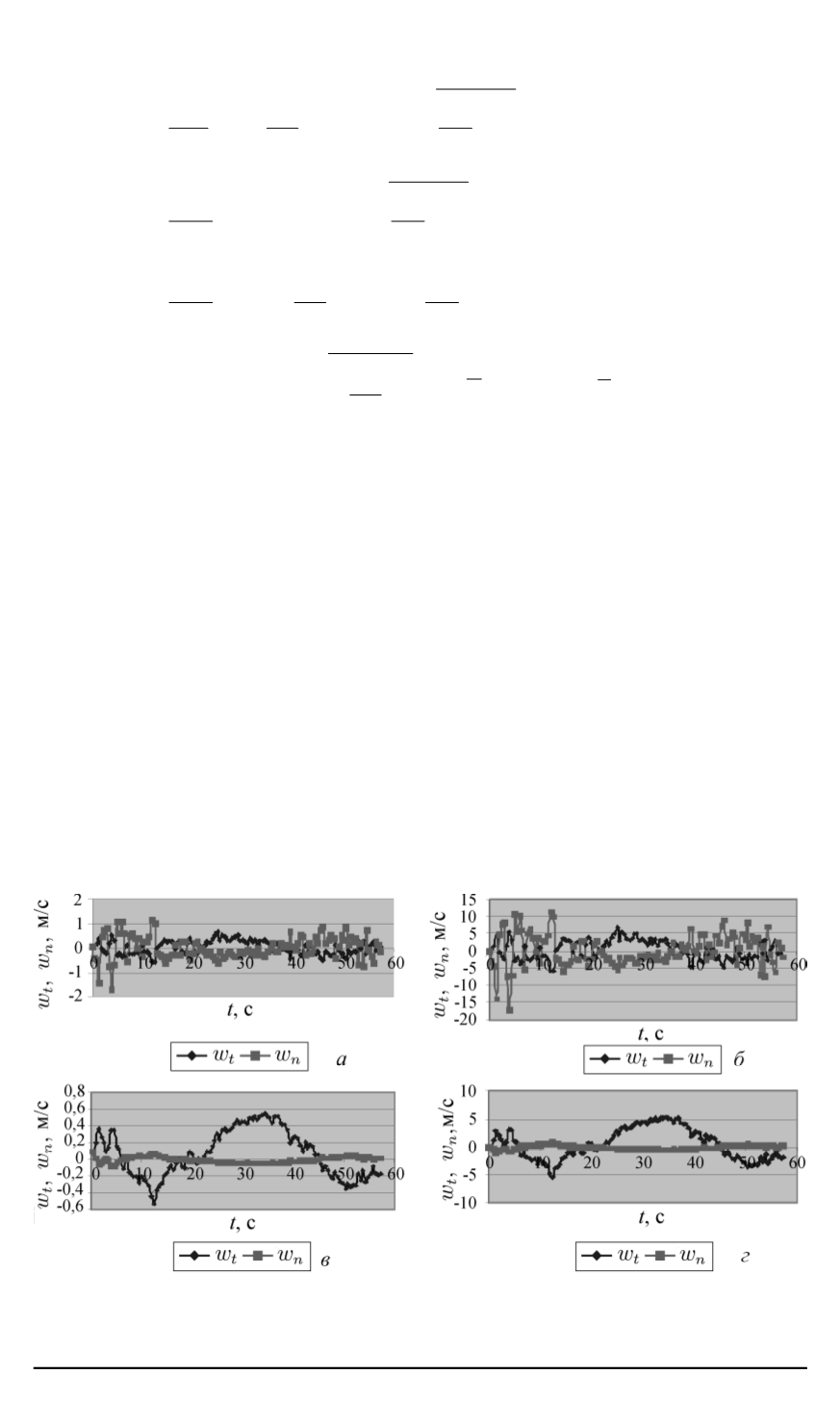
вить уравнения движения КБ. В качестве примера на рис. 1 показаны
результаты расчетов переменных составляющих скоростей ветра (
w
t
и
w
n
)
во время движения КБ (время полета составляет 57,78 c).
Рис. 1. Результаты расчетов переменных составляющих скоростей ветра (
w
t
и
w
n
)
:
L
T
— 150 м (
а, б
) и 2000 м (
в, г
);
σ
w
= 0
,
5
м/с (
а, в
) и 5 м/с (
б, г
)
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2008. № 3 41


