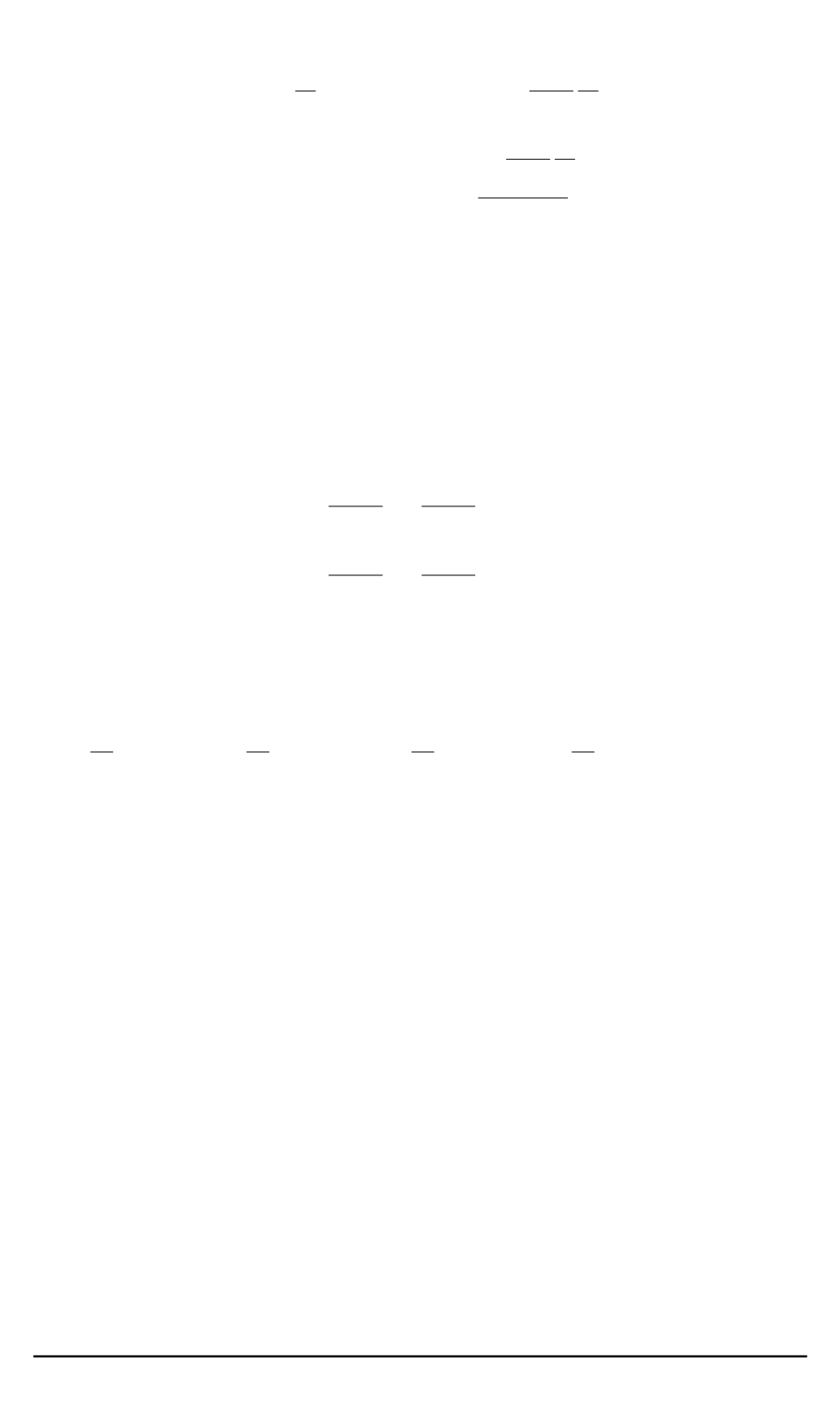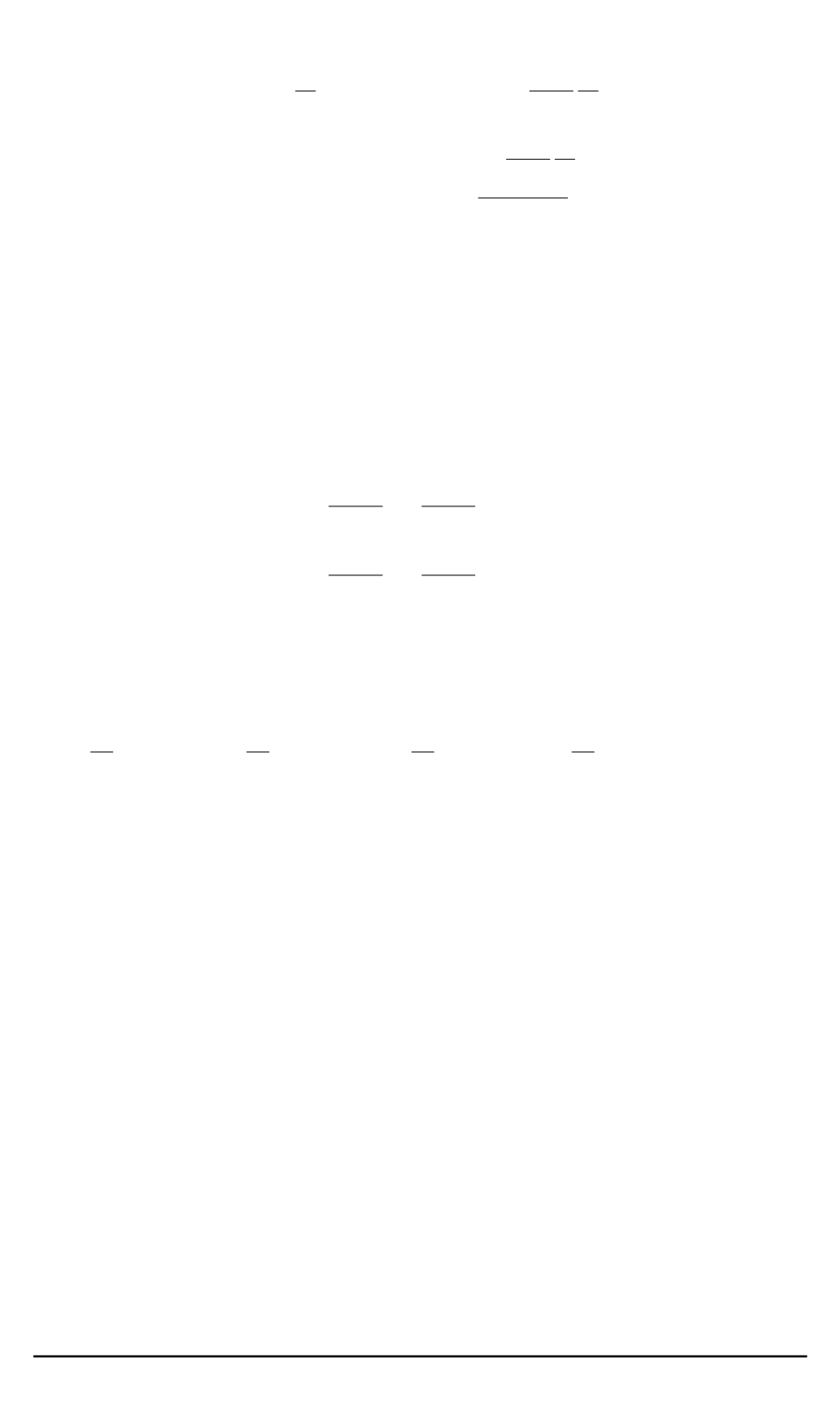
где
n
x
=
T
G
+ (
−
C
xa
+
C
α
ya
α
2
Σ
)
ρV
2
2
S
G
;
n
y
= (
C
xa
α
Σ
+
C
α
ya
α
Σ
)
ρV
2
2
S
G
;
α
Σ
= ˉ
α
h
+ ˉ
α
w
=
q
α
2
h
+
α
2
w
;
T
— тяга воздушного винта;
G
=
mg
— сила тяжести;
ˉ
α
h
и
ˉ
α
w
—
номинальное и ветровое значения углов атаки.
Имея в виду практическую невозможность получения требуемых
значений оценок с заданной точностью, можно реализовать принцип
оценивания с априори допустимой ограниченной неопределенностью
[1], сущность которого заключается в использовании линеаризованно-
го уравнения измерений вида
Δ
n
x
Δ
n
y
=
∂n
x
∂C
xa
∂n
x
∂C
α
ya
∂n
y
∂C
xa
∂n
y
∂C
α
ya
Δ
C
xa
Δ
C
α
ya
+
v,
(10)
где частные производные играют роль базисных функций,
v
— вектор
белых шумов, а для определения
Δ
m
α
z
,
Δ
m
ˉ
ω
z
z
,
Δ
C
xa
,
Δ
C
α
ya
использу-
ются уравнения формальных формирующих фильтров:
d
dt
Δ
m
α
z
= 0
,
d
dt
Δ
m
ˉ
ω
z
Z
= 0
,
d
dt
Δ
C
xa
= 0
,
d
dt
Δ
C
α
ya
= 0
.
(11)
Число реализаций процедуры метода статистических испытаний
ограничивается несколькими значениями исходя из априори введен-
ной допустимой погрешности оценивания при обязательном гаранти-
рованном получении результата в темпе полета.
Наличие остаточной (ограниченной) неопределенности диктует не-
обходимость применять в контуре управления полетом нечеткие ре-
гуляторы. Сущность подхода сводится к следующему. Контур упра-
вления ДПЛА предполагает использование четырех каналов: канала
управления высотой полета, регулирования скорости движения, а так-
же каналы управления углом крена и рулем направления. Последний
канал необходим для устранения угла скольжения по сигналу попе-
речной перегрузки.
Наиболее критичными являются каналы управления высотой и кре-
ном. Особенности конструкции рассматриваемого типа ДПЛА приве-
ли к необходимости дополнительной модификации обычного нечет-
кого регулятора за счет введения в закон управления приближенно-
го балансировочного значения угла отклонения руля высоты
δ
вгп
, по-
лученного в результате решения системы линейных алгебраических
62 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2013. № 3