
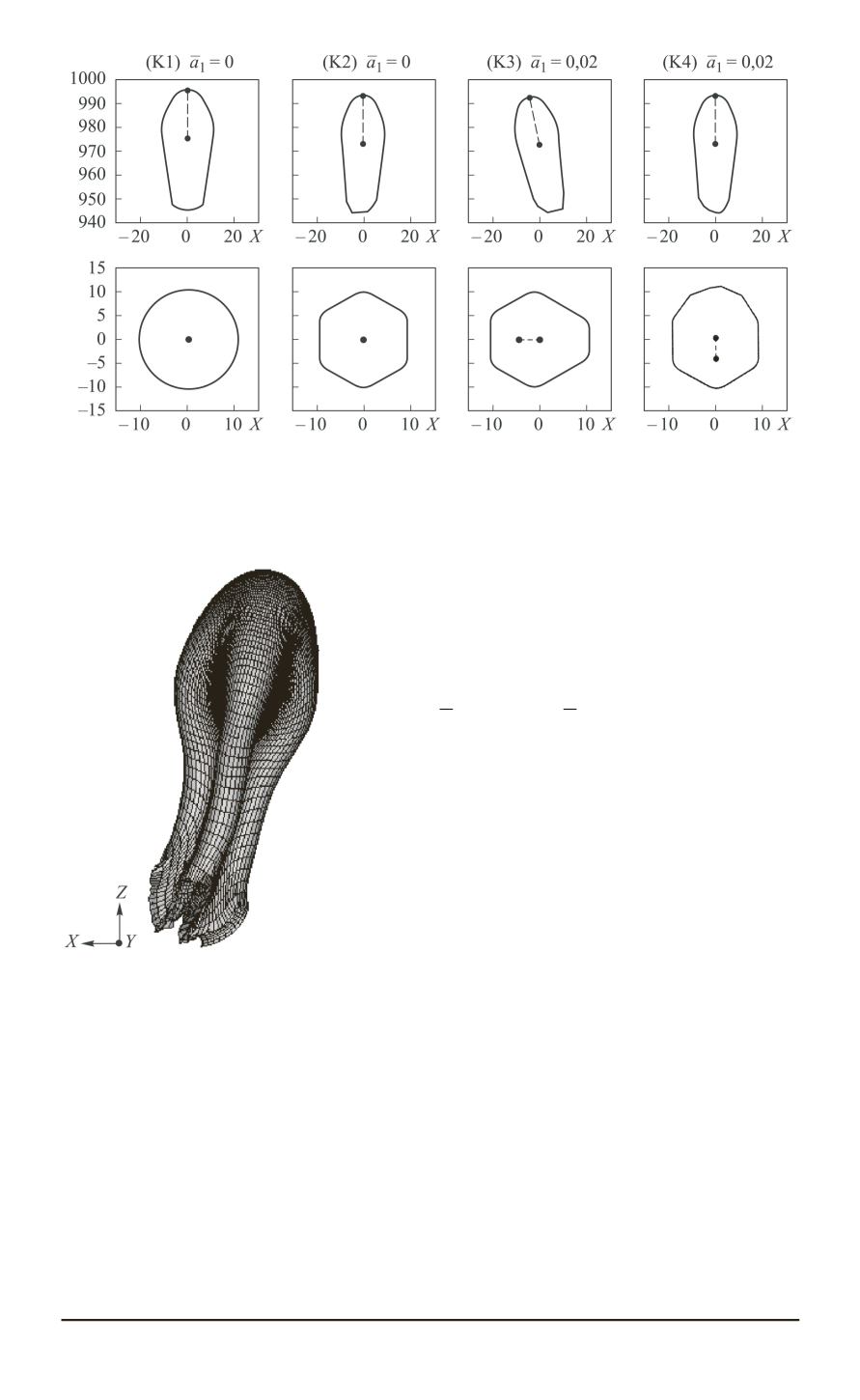
Рис. 6. Зависимость влияния погрешностей различных конфигураций на
форму ВСЭ (слева направо):
K1 — идеальная осесимметричная облицовка; K2 —
n
= 6
; K3 —
n
= 1
и 6 при
Δ
ψ
=
π/
3
; K4 —
n
= 1
и 6 при
Δ
ψ
= 0
Рис. 7. Изгиб ВСЭ при на-
личии двух гармонических
составляющих разностенно-
сти облицовки
Вследствие критического состояния ма-
териала в процессе формирования наиболее
вероятным результатом наличия погрешно-
стей значительной амплитуды является ис-
кажение формы и разрушение ВСЭ. Напри-
мер, при
a
1
= 0
,
05
и
a
6
= 0
,
03
на промежу-
точных этапах формирования ВСЭ наблю-
дался его изгиб, приводивший в послед-
ствие к разрушению ВСЭ (рис. 7).
Выводы.
1. Предложен подход к чи-
сленной оценке влияния погрешностей об-
лицовки на кинематические параметры
ВСЭ, основанный на внедрении неравно-
мерности малой амплитуды в дискретиза-
цию модели ВУ. Поскольку общепринятый
метод расчета задач формирования ВСЭ с
помощью подхода Эйлера не позволяет точ-
но описать границу тел, то был применен
подход Лагранжа. При этом параметры решателя были специально
адаптированы для задач с высокой скоростью деформаций, в част-
ности, применялся алгоритм удаления сильно искаженных элементов
с критически малым характерным размером. В рамках исследований
разработана математическая модель генерирования сетки облицовки с
контролируемыми погрешностями несоосности и разнотолщинности.
Разработан и реализован метод расчета параметров формы и кинема-
тики ВСЭ.
82 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2015. № 5

















