
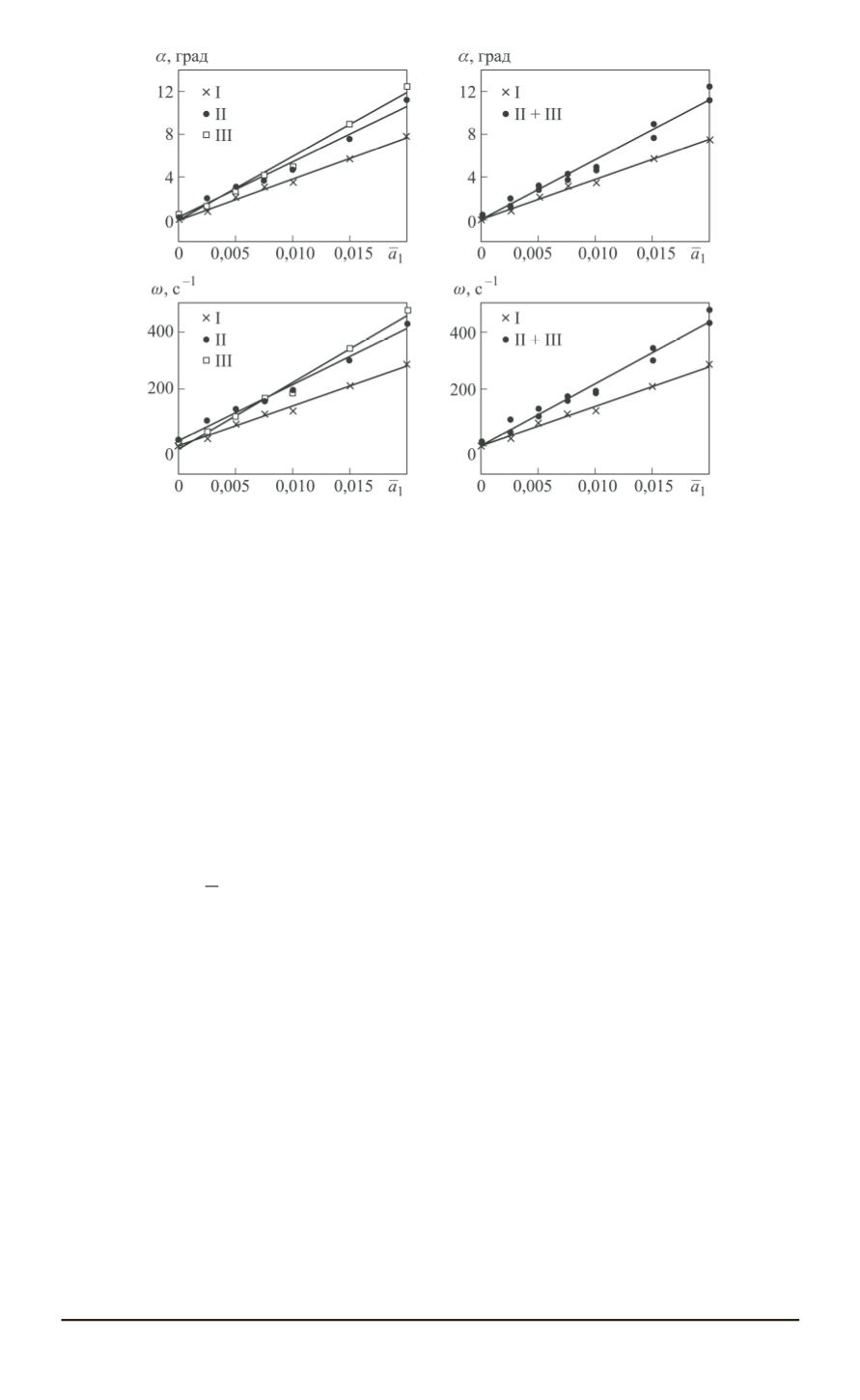
Рис. 5. Влияние суперпозиции гармоник разностенности на
α
и
ω
:
I — только несоосность; II —
Δ
ψ
=
π/
3
; III —
Δ
ψ
= 0
;
•
,
×
, — численные расчеты;
——— — регрессии
Очевидно также, что эффект от суперпозиции гармоник зависит от
разности фаз
Δ
ψ
=
|
ψ
1
−
ψ
6
|
между ними.
Расчеты не показали существенных различий во влиянии супер-
позиции гармоник на осевую
V
0
и радиальную
V
р
скорости ВСЭ по
сравнению с несоосностью наружной и внутренней поверхностей.
На рис. 5 (левые графики) приведено сравнение влияния несоосно-
сти на
α
и
ω
в условиях наличия одной и двух гармоник с различной
разностью фаз
Δ
ψ
. Характер зависимости для всех случаев имеет ли-
нейный вид (
ˆ
r >
0
,
99
для каждой отдельной конфигурации), но кон-
фигурации с суперпозицией гармоник более чувствительны к уровню
несоосности
a
1
. Коэффициент корреляции для конфигураций с су-
перпозицией гармоник вне зависимости от разности фаз составляет
ˆ
r
= 0
,
988
(см. рис. 5, правые графики).
Контуры элементов, сформированных из облицовок без погреш-
ностей и с погрешностями различной конфигурации, приведены на
рис. 6; ВСЭ, сформированный из облицовки идеальной формы (К1),
имеет ярко выраженную осевую симметрию. Наличие неравномерно-
сти толщины облицовки (
n
= 6
) приводит к образованию складок
(К2) при этом изменения угла
α
поворота элемента не происходит.
При суперпозиции гармоник
n
= 1
и
n
= 6
(К3 и К4) с различной раз-
ностью фаз
Δ
ψ
наблюдается наклон элемента с искажением формы
его кормовой части.
Полученные данные свидетельствуют о том, что наличие несколь-
ких гармонических составляющих погрешностей повышает чувстви-
тельность ВСЭ к их влиянию.
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение” 2015. № 5 81

















