
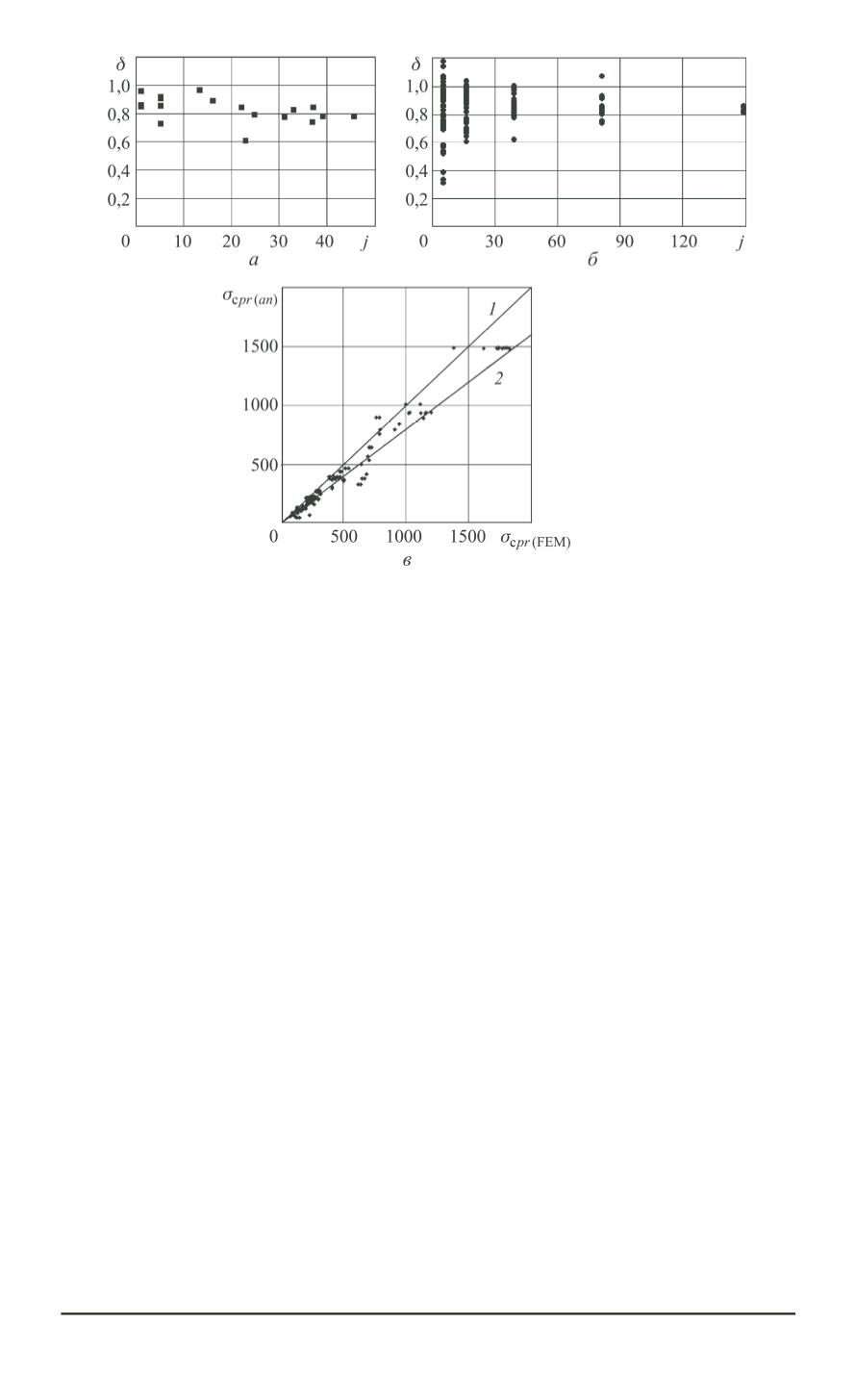
Рис. 4. Сопоставление результатов расчета по аналитической методике и МКЭ:
а
— распределение
δ
−
j
для моделей с оптимальным расположением ребра;
б
— то
же для моделей с неоптимальным расположением ребра;
в
— соотношение
σ
c
pr
(
an
)
и
σ
c
pr
(
FEM
)
в МПа для всех моделей
Как видно на графике (см. рис. 4,
б
), наибольшая погрешность ана-
литического расчета возникает в области малых значений
j <
15
при
неоптимальном расположении ребра. Это связано с тем, что в этих слу-
чаях возникают переходные формы потери устойчивости, когда одна
из панелей, теряя устойчивость, изгибает ребро, которое не имеет до-
статочной жесткости, чтобы удержать прямолинейный край панели.
В нормах [4] есть указание на то, что момент инерции ребра должен
удовлетворять условию
J
r
≥
1
,
5
dt
3
, что соответствует
j
≥
18
. Данное
ограничение учитывает не только отмеченное ранее обстоятельство,
но и негативное влияние сварки на местную устойчивость пластины
с ребром. Приварка ребра вызывает искривление ребра и пластины
и создает дополнительное поле напряжений, в котором сварной шов
будет растянут, а периферийные зоны пластины и ребра сжаты.
На основании приведенных данных можно утверждать, что пред-
ложенная методика позволяет прогнозировать устойчивость пластины
с двусторонним ребром при
j
≥
18
с погрешностью не более 20% в за-
пас надежности конструкции. Это вполне приемлемо для инженерных
приложений.
ЛИТЕРАТУРА
1.
Броуде Б.М.
Устойчивость пластинок в элементах стальных конструкций. М.:
Машстройиздат, 1949.
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение” 2015. № 4 127

















